
The following research codes are actively maintained:
Near the edge of tokamak plasmas, strong particle and energy sources and sinks (e.g. radiation, contact with a material wall,...) drive the plasma away from thermal equilibrium, thus invalidating the assumptions underpinning fluid theories. The XGC, gyrokinetic, particle-in-cell (PIC) suite-of-codes, XGC1, XGCa and XGC0, were developed to provide a comprehensive description of kinetic transport phenomena in this complicated region; including: heating and cooling, radiation losses, neutral particle recycling and impurity transport.
A particle's “state” is described by the position, ${\bf x}$, and velocity, ${\bf v}$; constituting a a six-dimensional phase space. Gyrokinetic codes average over the very-fast, “gyromotion” of charged particles in strong magnetic fields, ${\bf B}$, and phase space becomes five-dimensional, ${\bf X} \equiv ({\bf x},v_\parallel,\mu)$, where ${\bf x}$ is the position of the “guiding center”, $v_\parallel$ is the velocity parallel to ${\bf B}$, and $\mu$ is the “magnetic moment”. The density of particles is given by a distribution function, $f({\bf X},t)$; the evolution of which, including collisons, is formally described by the “Vlasov-Maxwell” equation: $f$ evolves along “characteristics”, which are the dynamical trajectories of the guiding centers [1], \begin{eqnarray} \dot {\bf x} & = & \left[ v_\parallel {\bf b} + v_\parallel^2 \nabla B \times {\bf b} + {\bf B} \times ( \mu \nabla B - {\bf E}) / B^2 \right] / D,\\ \dot v_\parallel & = & - ( {\bf B} + v_\parallel \nabla B \times {\bf b} ) \cdot ( \mu \nabla B - {\bf E}), \end{eqnarray} where ${\bf E}$ is the electric field, ${\bf b}={\bf B}/|B|$, and $D \equiv 1 + v_\parallel {\bf b} \cdot \nabla \times {\bf b}/B$ ensures the conservation of phase-space volume (Liouville theorem). The non-thermal-equilibrium demands that gyrokinetic codes must evolve the full distribution function, by applying classical “full-f” [2,3] and noise-reducing, “total-f” techniques [4]. (This is in contrast to so-called “$\delta f$” methods, which evolve only a small perturbation to an assumed-static, usually-Maxwellian distribution.) As full-f codes, XGC can include heat and torque input, radiation cooling; and neutral particle recycling [5].
Multiple particle-species (e.g. ions and electrons, ions and impurities) are included; and XGC uses a field-alligned, unstructured mesh in cylindrical coordinates, and so can easily accommodate the irregular magnetic fields in the plasma edge (e.g. the “X-point”, “separatrix”). XGC calculates transport in the entire plasma volume; from the “closed-flux-surface”, good-confinement region (near the magnetic axis) to the “scrape-off layer” (where magnetic fieldlines intersect the wall and confinement is lost). Collisions between ions, electrons and impurities are evaluated using either (i) a linear, Monte-Carlo operator [6] for test-particles, and the Hirshman-Sigmar operator [7] for field-particle collisions; or (ii) a fully-nonlinear, Fokker-Planck-Landau collision operator [8,9]. XGC codes efficiently exploit massively-parallel computing architecture.
Fusion energy gain in tokamaks depends sensitively on the plasma edge [1,2]; but, because of open- and closed-fieldlines, interaction with divertor plates, neutral particles, and large electromagnetic fluctuations, the edge region is, understandably, difficult to treat analytically. Large-scale, kinetic, numerical simulations are required. The “GKEYLL” code [3] is a flexible, robust, powerful, algorithm that provides numerical calculations of gyrokinetic turbulence, which importantly preserves the conservation laws of gyrokinetics.
Gyrokinetics [4] describes how a distribution of particles, described by a density-distribution function, $f(t,{\bf z})$, evolves in time, $t$; where ${\bf z}=({\bf x},{\bf v})$ describes the position and velocity, i.e. a point in “phase space”, of the guiding-center. Elegant theoretical and numerical descriptions of this dynamical system exploit the “Hamiltonian properties”, i.e. $\partial f / \partial t + \{f,H\} = 0$, where $H({\bf z})$ is the Hamiltonian (i.e. “energy”, e.g. for a Vlasov system, $H(x, v, t)$ $=$ $mv^2/2$ $+$ $q \, \phi(x,t)$, where $\phi$ is the electro-static potential) and $\{g,f\}$ is the Poisson bracket operator [5]. For reliable simulations, numerical discretizations must preserve so-called “quadratic invariants”, $\int H \{ f,H\} \, d{\bf z} $ $=$ $ \int f \{ f,H\} \, d{\bf z} = 0$.
Discontinuous Galerkin (DG) algorithms represent the “state-of-art” discretizations of hyperbolic, partial-differential equations [6]. DG combines the key advantages of finite-elements (e.g. low phase error, high accuracy, flexible geometries) with those of finite-volumes (e.g. up-winding, guaranteed positivity/monotonicity, . . . ), and makes efficient use of parallel computing architectures. DG is inherently super-convergent: e.g., whereas finite-volume methods interpolate $p$ points to get $p$-th order accuracy, DG methods in contrast interpolate $p$ points to get $(2p−1)$-th order accuracy, a significant advantage for $p>1$! Use of DG schemes may lead to significant advances towards a production-quality, edge gyrokinetic simulation software with reasonable computational costs.
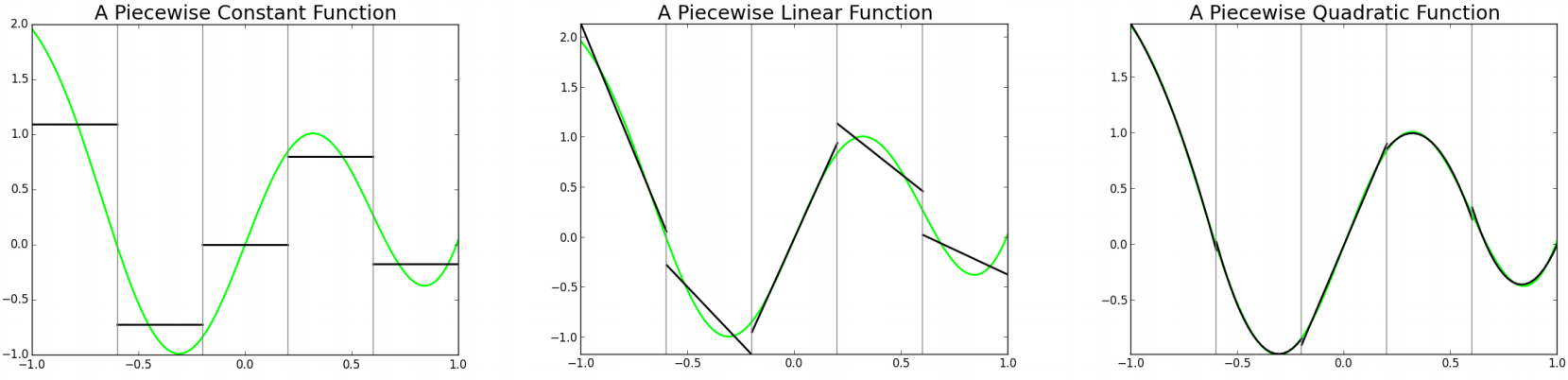
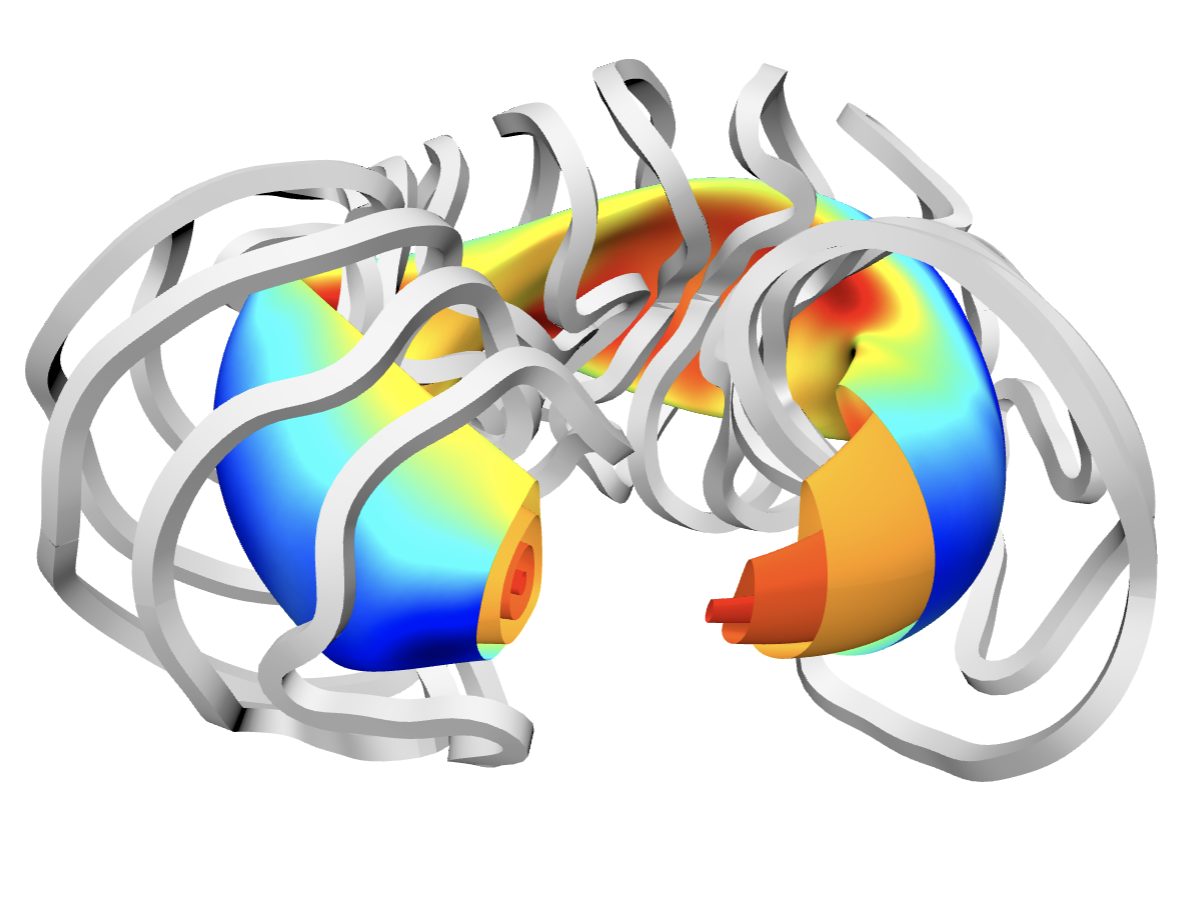
NOVA is a suite of codes including the linear ideal eigenmode solver to find the solutions of ideal magnetohydrodynamic (MHD) system of equations [1], including such effects as plasma compressibility and realistic tokamak geometry. The kinetic post-processor of the suite, NOVA-K [2], analyses those solutions to find their stability properties. NOVA-K evaluates the wave particle interaction of the eigenmodes such as Toroidal Alfvén Eigenmodes (TAEs) or Reversed Shear Alfvén Eigenmodes (RSAEs) by employing the quadratic form with the perturbed distribution function coming from the drift kinetic equations [2,4]. The hot particle growth rate of ideal MHD eigenmode is expressed via the equation \begin{eqnarray} \frac{\gamma_{h}}{\omega_{AE}}=\frac{\Im\delta W_{k}}{2\delta K}, \end{eqnarray} where $\omega_{AE}$ is Alfvén eigenmode frequency, $\delta W_{k}$ is the potential energy of the mode, and $\delta K$ is the inertial energy. In computations of the hot ion contribution to the growth rate NOVA-K makes use of the constant of motion to represent the hot particle drift orbits. Example of such representation is shown in the figure.
NOVA is routinely used for AE structure computations and comparisons with the experimentally observed instabilities [5,6]. The main limitations of NOVA code are caused by neglecting thermal ion finite Larmor radius (FLR), toroidal rotation, and drift effects for the eigenmode computations. Therefore it can not describe accurately radiative damping for example. Finite element methods are used in radial direction and Fourier harmonics are used in poloidal and toroidal directions.
NOVA-K is able to predict various kinetic growth and damping rates perturbatively, such as the phase space gradient drive from energetic particles, continuum damping, radiative damping, ion/electron Landau damping and trapped electron collisional damping.
More information can be found on Dr. N. N. Gorelenkov's NOVA page.
The guiding center code Orbit, using guiding center equations first derived in White and Chance [1] and more completely in The Theory of Toroidally Confined Plasmas [2], can use equal arc, PEST, or any other straight field line coordinates $\psi_p, \theta, \zeta$, which along with the parallel velocity and energy completely specify the particle position and velocity. The guiding center equations depend only on the magnitude of the $B$ field and functions $I$ and $g$ with $\vec{B} = g\nabla \zeta + I\nabla \theta + \delta \nabla \psi_p$. In simplest form, in an axisymmetric configuration, in straight field line coordinates, and without field perturbation or magnetic field ripple, the equations are \begin{eqnarray} \dot{\theta} = \frac{ \rho_{\parallel}B^2}{D} (1 - \rho_{\parallel}g^{\prime}) + \frac{g}{D}\left[ (\mu + \rho_{\parallel}^2B)\frac{\partial B}{\partial\psi_p} + \frac{\partial \Phi}{\partial\psi_p}\right], \label{tdot2} \end{eqnarray} \begin{eqnarray} \dot{\psi_p} = -\frac{g}{D}\left[(\mu +\rho_{\parallel}^2B)\frac{\partial B}{\partial\theta} + \frac{\partial \Phi}{\partial\theta}\right], \label{psdot2} \end{eqnarray} \begin{eqnarray} \dot{\rho_{\parallel}} = -\frac{(1 -\rho_{\parallel}g^{\prime})}{D} \left[(\mu +\rho_{\parallel}^2B)\frac{\partial B}{\partial\theta} + \frac{\partial\Phi}{\partial\theta}\right], \label{rdot2} \end{eqnarray} \begin{eqnarray} \dot{\zeta} = \frac{ \rho_{\parallel}B^2}{D} (q +\rho_{\parallel}I^{\prime}_{\psi_p}) - \frac{I}{D} \left[(\mu +\rho_{\parallel}^2B)\frac{\partial B}{\partial\psi_p} + \frac{\partial \Phi}{\partial\psi_p}\right], \label{zdot2} \end{eqnarray} with $ D = gq + I + \rho_\parallel(g I'_{\psi_p} - I g'_{\psi_p})$. The terms in $\partial \Phi/\partial\psi_p$, $\partial \Phi/\partial\theta$, $\partial \Phi/\partial\zeta$ are easily recognized as describing $\vec{E}\times \vec{B}$ drift.
Orbit can read numerical equilibria developed by TRANSP or other routines, particle distributions produced by TRANSP, and mode eigenfuncitons produced by NOVA.
The code uses a fourth order Runge Cutta integration routine. It is divided into a main program Orbit.F, which is essentially a heavily commented name list and a set of switches for choosing the type of run, the diagnostics, the data storage, and output.
The code has been used extensively since its inception at PPPL, General Atomics, RFX (Padova) and Kiev for the analysis of mode-induced particle loss for fishbones and TAE modes, induced ripple loss, the modification of particle distributions, local particle transport, etc.
To obtain a copy take all files from /u/ftp/pub/white/Orbit. To submit a job modify the script batch, modify Orbit.F to choose the run desired, type make, and type qsub -q sque batch

The Gyrokinetic Tokamak Simulation (GTS) code is a full-geometry, massively parallel $\delta f$ particle-in-cell code [1,2] developed at PPPL to simulate plasma turbulence and transport in practical fusion experiments. The GTS code solves the modern gyrokinetic equation in conservative form [3]: \begin{equation} \frac{\partial f_a}{\partial t}+\frac{1}{B^{*}}\nabla_{\bf Z}\cdot (\dot{{\bf Z}}B^{*}f_a)=\sum\limits_{b} C[f_a, f_b]. \end{equation} for a gyro-center distribution function $f ({\bf Z}, t)$ in 5-dimension phase space ${\bf Z}$, along with the gyrokinetic Poisson equation and Ampere's law for potentials using a $\delta f$ method.
GTS features high robustness at treating globally consistent, shaped cross-section tokamaks; in particular, the highly challenging spherical tokamak geometry such as NSTX and its upgrade NSTX-U. GTS simulations directly import plasma profiles of temperature, density and toroidal rotation from the TRANSP experimental database, along with the related numerical MHD equilibria, including perturbed equilibria. General magnetic coordinates and a field-line-following mesh are employed [1]. The particle gyro-center motion is calculated by Lagrangian equations in the flux coordinates, which allows for accurate particle orbit integration thanks to the separation between fast parallel motion and slow perpendicular drifts. The field-line-following mesh accounts for the nature of the quasi-2D mode structure of drift-wave turbulence in toroidal systems, and hence offers a highly efficient spatial resolution for strongly anisotropic fluctuations in fusion plasmas. Fully-kinetic electron physics is included. In particular, both trapped and untrapped electrons are included in the non-adiabatic response. GTS solves the field equations in configuration space for the turbulence potentials using finite element method on unstructured mesh, which is carried out by PETSc. The real space, global field solver, in principle, retains all toroidal modes from $(m,n) = (0,0)$ all the way up to a limit which is set by grid resolution, and therefore retains full-channel nonlinear energy couplings.
One remarkable feature in GTS, which distinguishes it from the other $\delta f$ particle simulations, is that the weight equations satisfy the incompressibility condition in extended phase space $({\bf Z}, w)$ [4]. Satisfying the incompressibility is actually required in order to correctly solve the $\delta f$ kinetic equation using simulation markers whose distribution function $F({\bf Z}, w, t)$ is advanced along the marker trajectory in the extended phase space according to $F({\bf Z},w,t)=const.$.
In GTS, Coulomb collisions between like particles are implemented via a linearized Fokker-Plank operator with particle, momentum and energy conservation. Electron-ion collisions are simulated by the Lorentz operator. By modeling the same gyrokinetic-Poisson system, GTS is extended to performing global neoclassical simulation in additional to traditional turbulence simulation. More importantly, GTS now is able to do a global gyrokinetic simulation with self-consistent turbulence and neoclassical dynamics coupled together. This remarkable capability is shown to lead to significant new features regarding nonlinear turbulence dynamics, impacting a number of important transport issues in tokamak plasmas. In particular, this capability is critical for the proposed study of nonlinear NTM physics. For example, it allows to calculate bootstrap current in the presence of turbulence [5, 6], which plays a key role for NTM evolution. Currently, GTS has been extended to simulating finite beta physics. This includes low-n shear-Alfvén modes, current driven tearing modes, kinetic ballooning modes and micro-tearing modes.
A state-of-the-art electromagnetic algorithm has been developed and implemented into GTS [7,8] with the goal to achieve a robust, global electromagnetic simulation capability to attack the highly challenging electron transport problem in high-$\beta$ NSTX-U plasmas and be used as a first-principles-based module for integrated whole device modeling of turbulence/neoclassical/MHD physics.
On the front of physics study, GTS simulations have been applied to wide experiments for various problems. Recent applications include discovering new turbulence sources responsible for plasma transport and understanding underlying physics behind the confinement scaling in spherical tokamak experiments [4,9], validating the physics of turbulence-driven plasma flow and first-principles-based model prediction of intrinsic rotation profile against profile against experiments [10], and plasma self-generated non-inductive current in turbulent fusion plasmas [5].
GTS has three levels of parallelism: a one-dimensional domain decomposition in the toroidal direction, dividing both the grid and the particles, a particle distribution within each domain, which further divides the particles between processors, and a loop-level multi-threading method. The domain decomposition and the particle distribution are implemented with MPI, while the loop-level multi-threading is implemented with OpenMP directives.

HMHD is a massively parallel, general purpose 3D extended MHD code that solves the fluid equations of particle density $n$ and momentum density $n\boldsymbol{u}$: \[ \partial_{t}n+\nabla\cdot\left(n\boldsymbol{u}\right)=0, \] \[ \partial_{t}\left(n\boldsymbol{u}\right)+\nabla\cdot\left(n\boldsymbol{uu}\right)=-\nabla\left(p_{i}+p_{e}\right)+\boldsymbol{J}\times\boldsymbol{B}-\nabla\cdot\boldsymbol{\Pi}+\boldsymbol{F}, \] where $\boldsymbol{J}=\nabla\times\boldsymbol{B}$ is the electric current, $p_{e}$ and $p_{i}$ are the electron and ion pressures, $\boldsymbol{\Pi}$ is the viscous stress tensor, and $\boldsymbol{F}$ is an external force. The magnetic field ${\bf B}$ is stepped by the Faraday's law \[ \partial_{t}\boldsymbol{B}=-\nabla\times\boldsymbol{E}, \] where the electric field $\boldsymbol{E}$ is determined by a generalized Ohm's law that incorporates the Hall term and the electron pressure term in the following form: \[ \boldsymbol{E}=-\boldsymbol{u}\times\boldsymbol{B}+d_{i}\frac{\boldsymbol{J}\times\boldsymbol{B}-\nabla p_{e}}{n}+\eta\boldsymbol{J}, \] with $\eta$ the resistivity and $d_{i}$ the ion skin depth. The set of equations is completed by additional equations for electron and ion pressures $p_{e}$ and $p_{i}$, where several options are available. In the simplest level an isothermal equation of state $p_{i}=p_{e}=nT$ is assumed; in a sophisticated level, the ion and electron pressure can be evolved individually with viscous and resistive heating, anisotropic thermal conduction, and thermal exchange between the two species; various additional options are available between these two levels. HMHD is flexible to switch on and off various effects in the governing equations.
HMHD uses a single Cartesian grid, with the capability of variable grid spacing. The numerical algorithm [1] approximates spatial derivatives by finite differences with a five-point stencil in each direction. The time-stepping scheme has several options including a second-order accurate trapezoidal leapfrog method as well as three-stage or four-stage strong stability preserving Runge-Kutta methods [2,3]. HMHD is written in Fortran 90 and parallelized with MPI for domain decomposition, augmented with OpenMP for multi-threading in each domain. HMHD has been employed to carry out large-scale 2D simulations plasmoid-mediated reconnection in resistive MHD [4,5,6] and Hall MHD [7,8]. It has been used to carry out 3D self-generated turbulent reconnection simulations [9,10].
Finding an easy-to-build coils set has been a critical issue for stellarator design for decades. The construction of the coils is only one component of modern fusion experiments; but, realizing that it is the currents in the coils that produce the “magnetic bottle” that confines the plasma, it is easy to understand that designing and accurately constructing suitable coils is paramount.
Conventional approaches simplify this problem by assuming that coils are lying on a defined toroidal “winding” surface [1]. The Flexible Optimized Coils using Space Curves (FOCUS) code [2] represents coils as one-dimensional curves embedded in three-dimensional space. A curve is described directly, and completely generally, in Cartesian coordinates as ${\bf x}(t) = x(t) \, {\bf i} + y(t) \, {\bf j} + z(t) \, {\bf k}$. The coil parameters, ${\bf X}$, are then varied to minimize a target function consisting of multiple objective functions, \begin{equation} \chi^2({\bf X}) \equiv w_{B}\int_S \frac{1}{2} \left ( { \bf B} \cdot {\bf n} \right )^2 ds \ + \ w_{\Psi}\int_0^{2\pi} \frac{1}{2} \left( \Psi_\zeta \; - \; \Psi_o \right)^2 d\zeta \ + \ w_{L} \; \sum_{i=1}^{N_C} L_i + \cdots \end{equation} These objective functions cover both “physics” requirements and “engineering” constraints, such as the normal magnetic field, the toroidal flux, the resonant magnetic harmonics, coil length, coil-to-coil separation and coil-to-plasma separation.
With analytically calculated derivatives, FOCUS computes the gradient and Hessian with respect to coil parameters fast and accurately. It allows FOCUS to employ numerous powerful optimization algorithms, like the Newton method [3]. The figure (click to enlarge) shows using FOCUS to design modular coils for a rotating elliptical stellerator. FOCUS is also applied to analyze the error field sensitivity to coil deviations [4], vary the shape of plasma surface in order to simplify the coil geometry [5] and design non-axisymmetric RMP coils for tokamaks.
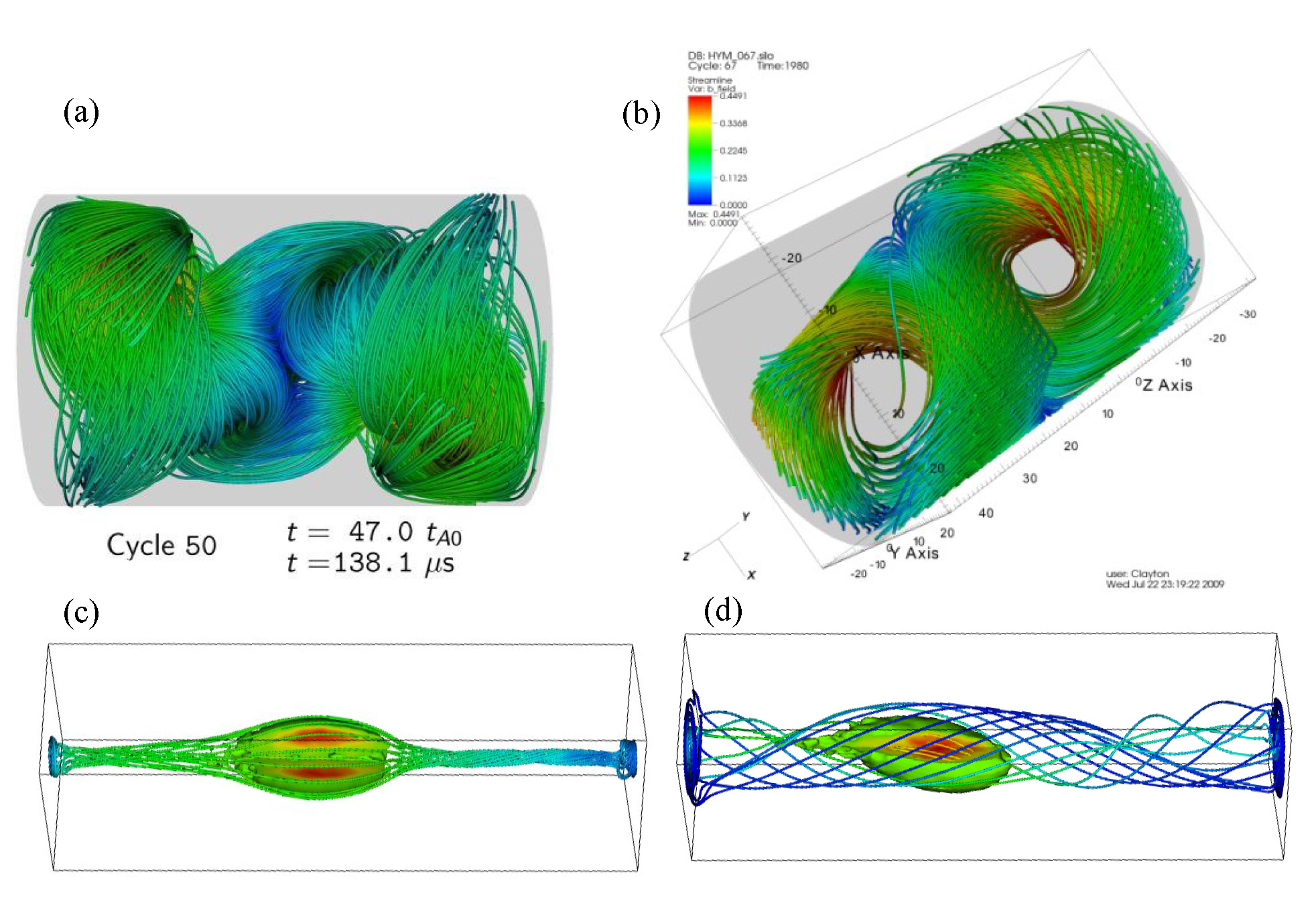
The nonlinear 3-D simulation code (HYM) has been originally developed at PPPL to carry out investigations of the macroscopic stability properties of FRCs [1,2]. The HYM code has also been used to study spheromak merging [3], and the excitation of sub-cyclotron frequency waves by the beam ions in the National Spherical Torus Experiment (NSTX) [4,5]. In the HYM code, three different physical models have been implemented: (a) a 3-D nonlinear resistive MHD or Hall-MHD model; (b) a 3-D nonlinear hybrid scheme with fluid electrons and particle ions; and (c) a 3-D nonlinear hybrid MHD/particle model where a fluid description is used to represent the thermal background plasma, and a kinetic (particle) description is used for the low-density energetic beam ions. The nonlinear delta-f method has been implemented in order to reduce numerical noise in the particle simulations. The capabilities of the HYM code also include an option to switch from the delta-f method to the regular particle-in-cell (PIC) method in the highly nonlinear regime. An MPI-based, parallel version of the HYM code has been developed to run on distributed-memory parallel computers. For production-size MHD runs, very good parallel scaling has been obtained for up to 1000 processors at the NERSC Computer Center. The HYM code has been validated against FRC experiments [6], SSX spheromak merging experiments [3], and NSTX and NSTX-U experimental results related to stability of sub-cyclotron frequency Alfven eigenmodes [4,5].
The HYM code is unique in that it employs the delta-f particle simulation method and a full-ion-orbit description in a toroidal geometry. Second-order, time-centered, explicit scheme is used for time stepping, with smaller time steps for field equations (subcycling). Fourth-order finite difference and cylindrical geometry are used to advance fields and apply boundary conditions, while a 3D Cartesian grid is used for the particle pushing and gathering of fast ion density and current density. Typically, the total energy is conserved within 10% of the wave energy, provided that the numerical resolution is sufficient for the mode of interest. Both 3D hybrid simulations of spheromak merging and 3D simulations of the FRC compression require use of a full-f simulation scheme, and therefore a large number of simulation particles. The HYM code has been modified in order to allow simulations with up to several billions of simulation particles.
The initial equilibrium used in the HYM code is calculated using a Grad-Shafranov solver. The equilibrium solver allows the computation of MHD equilibria including the effects of toroidal flows [1]. In addition, the MPI version of the Grad-Shafranov solver has been developed for kinetic equilibria with a non-Maxwellian and anisotropic ion distribution function [7].
The ability to choose between different physical models implemented in the HYM code facilitates the study of a variety of physical effects for a wide range of magnetic configurations. Thus, the numerical simulations have been performed for both oblate and prolate field-reversed configurations, with elongation in the range E=0.5-12, in both kinetic and MHD-like regimes; in support of co-helicity and counter-helicity spheromak merging experiments; for rotating magnetic field (RMF) FRC studies; and investigation of the effects of neutral beam injection (NBI) ions on FRC stability. In addition, hybrid simulations using the HYM code have predicted for the first time, destabilization of the Global Alfven Eigenmodes (GAEs) by the energetic beam ions in the National Spherical Torus Experiment (NSTX) [8], subsequently confirmed both by the analytical calculations and the experimental observations, and suggested a new energy channeling mechanism explaining flattening of the electron temperature profiles at high beam power in NSTX [4].
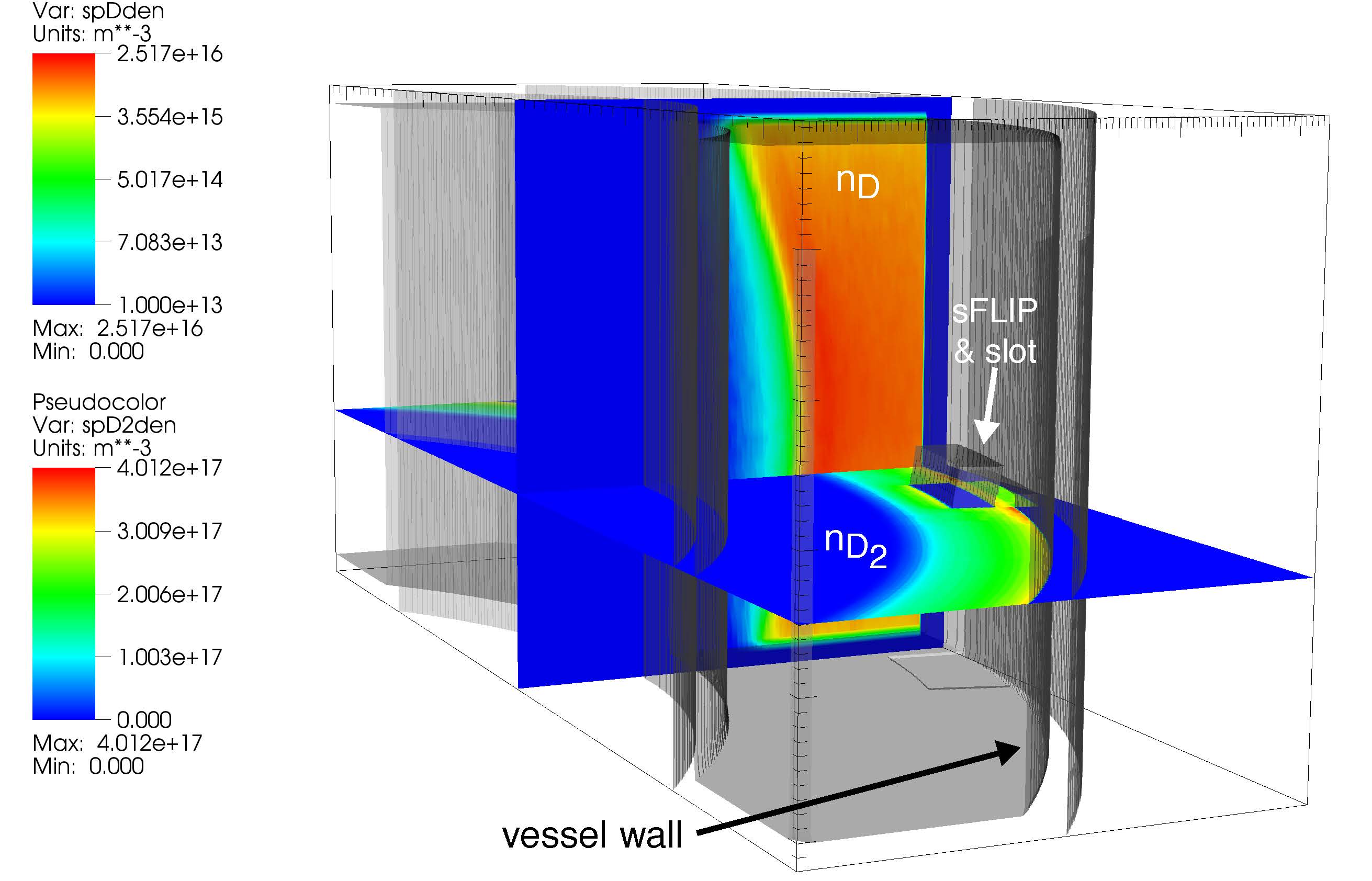
Neutral atoms and molecules in fusion plasmas are of interest for multiple reasons. First, neutral particles are produced via the interactions of the plasma as it flows along open field lines to surrounding material surfaces. Unconfined by the magnetic field, the atoms and molecules provide a channel for heat transport across the field lines and also serve as a source of plasma particles via ionization. Second, atoms that penetrate well past the last closed flux surface can charge exchange with plasma ions to generate high energy neutrals that can strike the vacuum vessel wall, sputtering impurities into the plasma and possibly damaging the wall. Third, the most common means of fueling plasmas is with an external puff of gas. Finally, the light emitted by the neutral atoms and molecules in all of the above processes can be monitored and used as the basis for diagnostics.
Kinetic models of neutral particle transport are based on the Boltzmann equation. For the simple case of a single ``background'' species and a single binary collision process, this is: \begin{eqnarray*} \frac{\partial f({\bf r}, {\bf v}, t)}{\partial t} & + & {\bf v} \cdot \nabla_{\bf r} f({\bf r}, {\bf v}, t) \\ & = & \int d{\bf v}^{\prime} \, d{\bf V}^{\prime} \, d{\bf V} \sigma( {\bf v}^{\prime}, {\bf V}^{\prime}; {\bf v}, {\bf V}) | {\bf v}^{\prime} - {\bf V}^{\prime} | f({\bf v}^{\prime}) f_{b}({\bf V}^{\prime}) \\ & - & \int d{\bf v}^{\prime} \, d{\bf V}^{\prime} \, d{\bf V} \sigma( {\bf v}, {\bf V}; {\bf v}^{\prime}, {\bf V^{\prime}}) | {\bf v} - {\bf V} | f({\bf v}) f_{b}({\bf V}), \label{BE} \end{eqnarray*} where $f({\bf r}, {\bf v}, t)$ and $f_{b}({\bf r}, {\bf V}, t)$ are the neutral and background distribution functions, respectively, and $\sigma$ is the differential cross section for the collision process. The first (second) integral on the right-hand side represents scattering into (out of) the velocity $v$.
DEGAS 2 [1], like its predecessor, DEGAS [2], uses the Monte Carlo approach to integrating the Boltzmann equation, allowing the treatment of complex geometries, atomic physics, and wall interactions. DEGAS 2 is written in a ``macro-enhanced'' version of FORTRAN via the FWEB library, providing an object oriented capability and simplifying tedious tasks, such as dynamic memory allocation and the reading and written of self-describing binary files. As a result, the code is extremely flexible and can be readily adapted to problems seemingly far removed from tokamak divertor physics, e.g., its use in simulating the diffusive evaporation of lithium in NSTX [3] and LTX [4]. DEGAS 2 has been extensively verified, as is documented in its User's Manual [5]. Experimental validation has been largely centered on the Gas Puff Imaging (GPI) technique for visualizing plasma turbulence in the tokamak edge. The validation against deuterium gas puff data from NSTX is described in the paper by B. Cao et al. [6] Analogous work with both deuterium and helium has been carried out on Alcator C-Mod. A related application of DEGAS 2 is in the interpretation of data from the Edge Neutral Density Diagnostic on NSTX [7] and NSTX-U. DEGAS 2 has been applied to many other devices, including JT-60U [8], ADITYA [9], and FRC experiments at Tri-Alpha Energy [10]. Neutral transport codes are frequently coupled to plasma simulation codes to allow a self-consistent plasma-neutral solution to be computed. Initially, DEGAS 2 was coupled to UEDGE [11]. More recently, DEGAS 2 has been coupled to the drift-kinetic XGC0 [12], and has been used in the development and testing of the simplified built-in neutral transport module in XGC1 [13]. A related project is a DEGAS 2-based synthetic GPI diagnostic for XGC1 [14].
The accurate calculation of the equilibrium, stability and dynamical evolution of magnetically-confined plasma is fundamental for fusion research. The most suitable, macroscopic model to address some of the most critical challenges confronting tokamak plasmas is given by the extended-magnetohydrodynamic (MHD) equations, which describe plasmas as electrically conducting fluids of ions and electrons. The M3D-C$^1$ code [?] solves the fluid equations: for example, the “single-fluid” model, in which the ions and electrons are considered to have the same fluid velocity and temperature, the dynamical equations for the particle number density $n$, the fluid velocity $\vec{u}$, the total pressure $p$ are \begin{eqnarray} \frac{\partial n}{\partial t} + \nabla \cdot (n \vec{u}) & = & 0 \\ n m_i \left( \frac{\partial \vec{u}}{\partial t} + \vec{u} \cdot \nabla \vec{u} \right) & = & \vec{J} \times \vec{B} - \nabla p \color{blue}{ - \nabla \cdot \Pi + \vec{F}} \\ \frac{\partial p}{\partial t} + \vec{u} \cdot \nabla p + \Gamma p \nabla \cdot \vec{u} & = & \color{blue}{(\Gamma - 1) \left[Q - \nabla \cdot \vec{q} + \eta J^2 - \vec{u} \cdot \vec{F} - \Pi : \nabla u \right]} \end{eqnarray} together with a “generalized Ohm's law”, $\vec{E} = - \vec{u} \times \vec{B} \color{blue}{ + \eta \vec{J}}$; and with a reduced set of Maxwell's equations for the electrical-current density, $\vec{J} = \nabla \times \vec{B} / \mu_0$, and for the time evolution of the magnetic field, $\partial_t \vec{B} = - \nabla \times \vec{E}$. The manifestly divergence-free magnetic field, $\vec{B}$, and the fluid velocity, $\vec{u}$, are represented using stream functions and potentials, $\vec{B} = \nabla \psi \times \nabla \varphi + F \nabla \varphi$ and $\vec{u} = R^2 \nabla U \times \nabla \varphi + R^2 \omega \nabla \varphi + R^{-2} \nabla_\perp \chi$.
The “ideal-MHD” model is described by the above equations with the terms in blue set to zero. M3D-C$^1$ is also capable of computing the “two-fluid model”, which accommodates differences in the ion and electron fluid velocities: the generalized Ohm's law is augmented with $\color{red}{( \vec{J} \times \vec{B} - \nabla p_e - \nabla \cdot \Pi_e + \vec{F}_e ) / n_e}$, additional terms must be added to $\partial_t p$, and an equation for the “electron pressure”, $p_e$, must be included.
Physically-meaningful, “reduced” models provide accurate solutions in certain physical limits and are obtained, at a fraction of the computational cost, by restricting the scalar fields that are evolved: e.g., the two-field, reduced model is obtained by only evolving $\psi$ and $U$, and the “four-field”, reduced model by only evolving $\psi$, $U$, $F$, and $\omega$.
To obtain accurate solutions efficiently, over a broad range of temporal and spatial scales, M3D-C1 employs advanced numerical methods, such as: high-order, $C^1$, finite elements, an unstructured geometrical mesh, fully-implicit and semi-implicit time integration, physics-based preconditioning, domain-decomposition parallelization, and the use of scalable, parallel, sparse, linear algebra solvers.
M3D-C$^1$ is used to model numerous tokamak phenomena, including: edge localized modes (ELMs) [1]; sawtooth cycles [2]; and vertical displacement events (VDEs), resistive wall modes (RWMs), and perturbed (i.e. three-dimensional, 3D) equilibria [3].
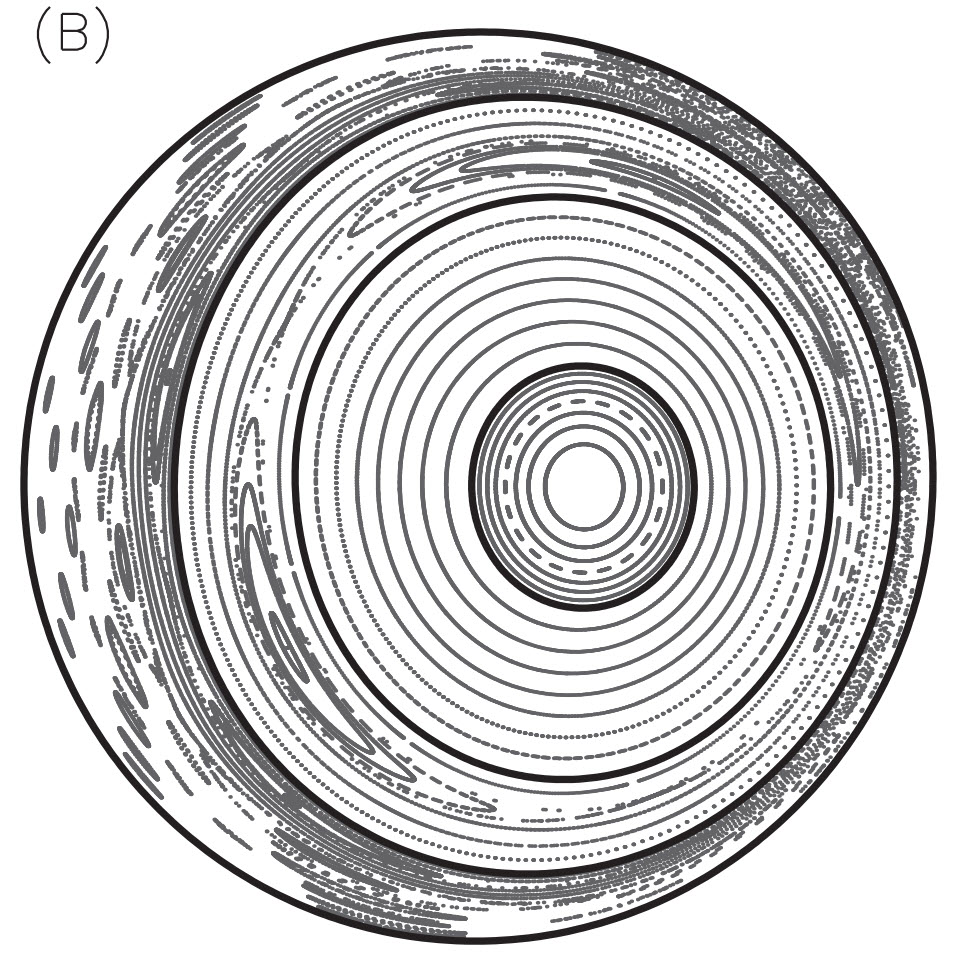
Building on the theoretical foundations of Bruno & Laurence [1], that three-dimensional, (3D) magnetohydrodynamic (MHD) equilibria with “stepped”-pressure profiles are well-defined and guaranteed to exist, whereas 3D equilibria with integrable magnetic-fields and smooth pressure (or with non-integrable fields and continuous-but-fractal pressure) are pathological [2], Dr. S.R. Hudson wrote the “Stepped Pressure Equilibrium Code”, (SPEC) [3]. SPEC finds minimal-plasma-energy states, subject to the constraints of conserved helicity and fluxes in a collection, $i=1, N_V$, of nested sub-volumes, ${\cal R}_i$, by extremizing the multi-region, relaxed-MHD (MRxMHD), energy functional, ${\cal F}$, introduced by Dr. M.J. Hole, Dr. S.R. Hudson & Prof. R.L. Dewar [4,5], \begin{eqnarray} {\cal F} \equiv \sum_{i=1}^{N_V} \left\{ \int_{{\cal R}_i} \! \left( \frac{p}{\gamma-1} + \frac{B^2}{2} \right) dv - \frac{\mu_i}{2} \left( \int_{{\cal R}_i} \!\! {\bf A}\cdot{\bf B} \, dv - H_i \right) \right\}. \end{eqnarray} Relaxation is allowed in each ${\cal R}_i$, so unphysical, parallel currents are avoided and magnetic reconnection is allowed; and the ideal-MHD constraints are enforced at selected “ideal interfaces”, ${\cal I}_i$, on which ${\bf B}\cdot{\bf n}=0$. The Euler-Lagrange equations derived from $\delta {\cal F}=0$ are: $\nabla \times {\bf B} = \mu_i {\bf B}$ in each ${\cal R}_i$; and continuity of total pressure, $[[p+B^2/2]]=0$, across each ${\cal I}_i$, so that non-trivial, stepped pressure profiles may be sustained. If $N_V=1$, MRxMHD equilibria reduce to so-called “Taylor states” [6]; and as $N_V \rightarrow \infty$, MRxMHD equilibria approach ideal-MHD equilibria [7]. Discontinuous solutions are admitted. The figure (click to enlarge) shows an $N_V=4$ equilibrium with magnetic islands, chaotic fieldlines and a non-trivial pressure.

Electrical currents flowing inside magnetically-confined plasmas cannot produce the magnetic field required for the confinement of the plasma itself. Quite aside from understanding the physics of plasmas, the task of designing external, current-carrying coils that produce the confining magnetic field, ${\bf B}_C$, remains a fundamental problem; particularly for the geometrically-complicated, non-axisymmetric, “stellarator” class of confinement device [1]. The coils are subject to severe, engineering constraints: the coils must be “buildable”, and at a reasonable cost; and the coils must be supported against the forces they exert upon each other. For reactor maintenance, the coils must allow access to internal structures, such as the vacuum vessel, and must allow room for diagnostics; many, closely-packed coils that give precise control over the external magnetic field might not be satisfactory.
The COILOPT code [2] and its successor, COILOPT++ [3], vary the geometrical degrees-of-freedom, ${\bf x}$, of a discrete set of coils to minimize a physics+engineering, “cost-function”, $\chi({\bf x})$, defined as the surface integral over a given, “target”, plasma boundary, ${\cal S}$, of the squared normal component of the “error” field, \begin{eqnarray} \chi^2 \equiv \oint_{\cal S} \left( \delta {\bf B} \cdot {\bf n} \right)^2 da + \mbox{engineering constraints}, \end{eqnarray} where $\delta {\bf B} \equiv {\bf B}_C - {\bf B}_P$ is the difference between the externally-produced magnetic field (as computed using the Biot-Savart law [5]) and the magnetic field, ${\bf B}_P$, produced by the plasma currents (determined by an equilibrium calculation). Using mathematical optimization algorithms, by finding an ${\bf x}$ that minimizes $\chi^2$ we find a coil configuration that minimizes the total, normal magnetic field at the boundary; thereby producing a “good flux surface”.
A new design methodology [3] has been developed for “modular” coils for so-called “quasi-axisymmetric” stellarators (stellarators for which the field strength appears axisymmetric in appropriate coordinates), leading to coils that are both simpler to construct and that allow easier access [4]. By straightening the coils on the outboard side of the device, additional space is created for insertion and removal of toroidal vessel segments, blanket modules, and so forth. COILOPT++ employs a “spline+straight” representation, with fast, parallel optimization algorithms (e.g. the Levenberg-Marquardt algorithm [6], differential evolution [7], ...), to quickly generate coil designs that produce the target equilibrium. COILOPT++ has allowed design of modular coils for a moderate-aspect-ratio, quasi-axisymmetric, stellarator reactor configuration, an example of which is shown in the figure (click to enlarge).
One of the defining characteristics of the “stellarator” class of magnetic confinement device [1] is that the confining magnetic field is, for the most part, generated by external, current-carrying coils; stellarators are consequently more stable than their axisymmetric, “tokamak” cousins, for which an essential component of the confining field is produced by internal plasma currents. Stellarators have historically had degraded confinement, as compared to tokamaks, and require more-complicated, “three-dimensional” geometry; however, by exploiting the three-dimensional shaping of the plasma boundary (which in turn determines the global, plasma equilibrium), stellarators may be designed to provide optimized plasma confinement. This is certainly easier said-than-done: the plasma equilibrium is a nonlinear function of the boundary, and the particle and heat transport are nonlinear functions of the plasma equilibrium!
STELLOPT [2,3] is a versatile, optimization code that constructs suitable, magnetohydrodynamic equilibrium states via minimization of a “cost-function”, $\chi^2$, that quantifies how “attractive” an equilibrium is; for example, $\chi^2$ quantifies the stability of the plasma to small perturbations (including “ballooning” stability, “kink” stability) and the particle and heat transport (including “neoclassical” transport, “turbulent” transport, “energetic particle” confinement). The independent, degrees-of-freedom, ${\bf x}$, describe the plasma boundary, which is input for the VMEC equilibrium code [4]. The boundary shape is varied (using either a Levenberg-Marquardt [5], Differential-Evolution [6] or Particle-Swarm [7] algorithms) to find minima of $\chi^2$; thus constructing an optimal, plasma equilibrium with both satisfactory stability and confinement properties.
A recent extension of STELLOPT enables “equilibrium reconstruction” [8,9]. By minimizing $\chi^2({\bf x})$ $\equiv$ $\sum_{i} [ y_i - f_i({\bf x}) ]^2 / \sigma_i^2$, where the $y_i$ and the $f_i({\bf x})$ are, respectively, the experimental measurements and calculated “synthetic diagnostics” (i.e. numerical calculations that mimic signals measured by magnetic sensors) of Thomson scattering, charge exchange, interferometry, Faraday rotation, motional Stark effect, and electro-cyclotron emission reflectometry, to name just a few, STELLOPT solves the “inverse” problem of inferring the plasma state given the experimental measurements. (The $\sigma_i$ are user-adjustable “weights”, which may reflect experimental uncertainties.) Equilibrium reconstruction is invaluable for understanding the properties of confined plasmas in present-day experimental devices, such as the DIIID device [10].