Transport processes play a very important role in the performance of fusion devices. Transport processes in plasmas transfer energy, mass and charge spatially, via collisions between particles or by flows, to bring a system towards thermodynamical equilibrium with its surroundings. Research on transport processes is intense, and may lead to great advances in commercial fusion reactor designs while already affording a better understanding of current experiments.
For turbulence transport, free energy is dissipated by chaotic flows, which are themselves usually generated by instabilities in the plasma. Turbulent transport is very effective in transporting energy and mass, and advances in large scale computing have enabled turbulent phenomena to be investigated in some detail.
Fusion energy gain in tokamaks depends sensitively on the plasma edge [1,2]; but, because of open- and closed-fieldlines, interaction with divertor plates, neutral particles, and large electromagnetic fluctuations, the edge region is, understandably, difficult to treat analytically. Large-scale, kinetic, numerical simulations are required. The “GKEYLL” code [3] is a flexible, robust, powerful, algorithm that provides numerical calculations of gyrokinetic turbulence, which importantly preserves the conservation laws of gyrokinetics.
Gyrokinetics [4] describes how a distribution of particles, described by a density-distribution function, $f(t,{\bf z})$, evolves in time, $t$; where ${\bf z}=({\bf x},{\bf v})$ describes the position and velocity, i.e. a point in “phase space”, of the guiding-center. Elegant theoretical and numerical descriptions of this dynamical system exploit the “Hamiltonian properties”, i.e. $\partial f / \partial t + \{f,H\} = 0$, where $H({\bf z})$ is the Hamiltonian (i.e. “energy”, e.g. for a Vlasov system, $H(x, v, t)$ $=$ $mv^2/2$ $+$ $q \, \phi(x,t)$, where $\phi$ is the electro-static potential) and $\{g,f\}$ is the Poisson bracket operator [5]. For reliable simulations, numerical discretizations must preserve so-called “quadratic invariants”, $\int H \{ f,H\} \, d{\bf z} $ $=$ $ \int f \{ f,H\} \, d{\bf z} = 0$.
Discontinuous Galerkin (DG) algorithms represent the “state-of-art” discretizations of hyperbolic, partial-differential equations [6]. DG combines the key advantages of finite-elements (e.g. low phase error, high accuracy, flexible geometries) with those of finite-volumes (e.g. up-winding, guaranteed positivity/monotonicity, . . . ), and makes efficient use of parallel computing architectures. DG is inherently super-convergent: e.g., whereas finite-volume methods interpolate $p$ points to get $p$-th order accuracy, DG methods in contrast interpolate $p$ points to get $(2p−1)$-th order accuracy, a significant advantage for $p>1$! Use of DG schemes may lead to significant advances towards a production-quality, edge gyrokinetic simulation software with reasonable computational costs.
The wave vectors of “probing”, electromagnetic waves propagating in plasmas depends, locally, on the electron density; therefore, the total phase-change of the waves after exciting the plasma provides information on the density variations within the plasma.
The phase-change of reflected waves, if these waves are reflected, is particularly sensitive to the density variation near the reflection layer.
Quantitative assessment of the multi-dimensional, geometric effects (e.g. curvature of the reflecting surface, refraction, diffraction, variation of the magnetic field direction, antenna geometries,...) determines the relationship between the measured signals and the turbulent, density fluctuations.
Using an ensemble of simulation calculations, and statistical analyses (e.g. the coherence and cross-correlations), a “synthetic” signal is predicted and compared to experimental meausurements.
The computational effort is enormous!
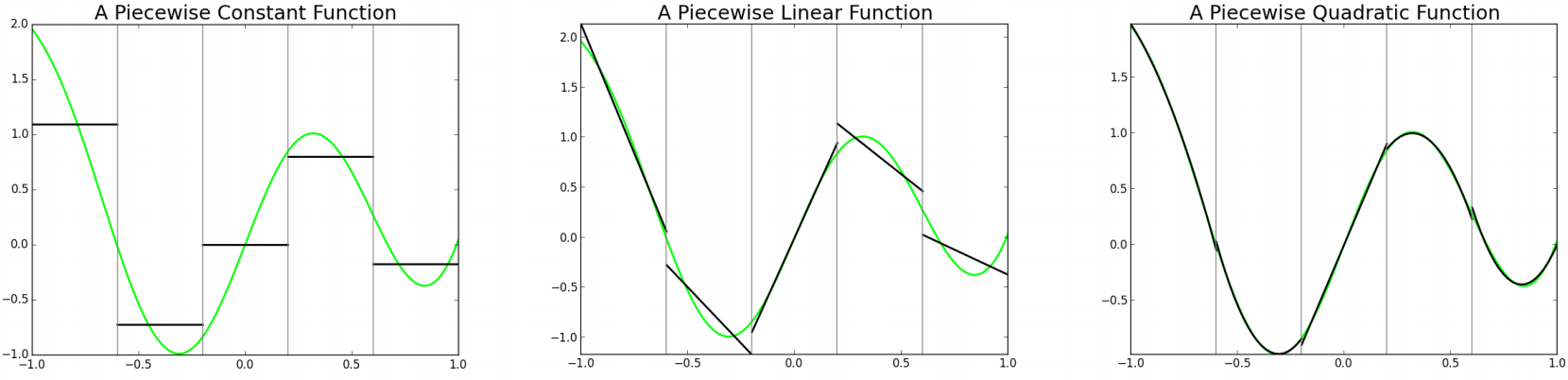
The two-dimensional, “Full-Wave, Reflectometry” simulation code, FWR2D [1], has been used to: (i) interpret data from the National Spherical Torus Experiment (NSTX) [2] and CMOD; (ii) help optimize DIIID imaging reflectometry configurations [3]; and (iii) to investigate the effects of the reflection-layer shift due to the relativistic electron-mass increase at high electron temperature, $T_e$, [4] in the next-generation-tokamak ITER [5]. Recently, FWR2D was extended to three-dimensional geometry, FWR3D [6]. A multiple-domain method is used; in which the demanding, full-wave equations are solved only in a narrow layer surrounding the reflection surface, and this greatly reduces the computational demands. Optimization of the low-field-side, ITER, reflectometer configuration, using FWR3D, is in progress: the received, signal-strength pattern (magenta) and amplitude (in db) at each of six, proposed, receiver locations is shown in the figure (click to enlarge) for one realization of turbulent, field-aligned density fluctuations at wavelength $\sim 1cm^{-1}$, and amplitude $\delta n / n = 0.05$, for a 30GHz “O” mode reflectometry in an H-mode ITER [5] profile. The orange ellipse shows the reflected intensity pattern in the absence of fluctuations.
Experiments show [1] that the confinement properties in the edge region of tokamaks determine the fusion performance in the core; consequently, predictive understanding of edge transport is a priority for ITER [2]. However, a theoretical understanding of edge transport is difficult because of the strong sources and sinks resulting from neutral particles and wall-loss, neoclassical and neutral particle physics, turbulence, and other effects that create a non-thermal (i.e. non-Maxwellian) equilibrium. The conventional, so-called $\delta f$ gyrokinetic method [3], which assumes a Maxwellian background plasma and is applicable for the plasma core, is thus not applicable for the plasma edge.
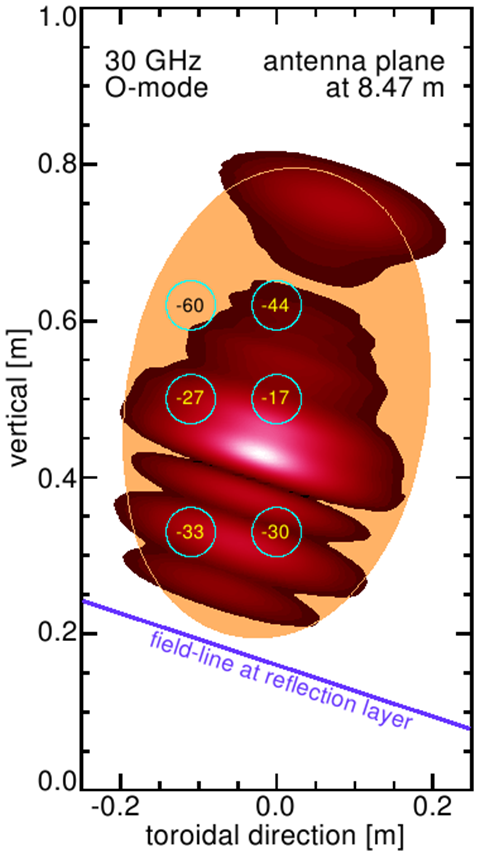
A new, “hybrid-Lagrangian” $\delta f$ gyrokinetic simulation method for studying the non-thermal, tokamak edge plasmas that are in contact with arbitrarily-shaped material-walls has been introduced [4] that takes advantage of the strengths of both particle and continuum methods, and that augments the weakness of both the $\delta f$ and the so-called full-$f$ methods. Averaging over the fast gyro-motion, phase space becomes five-dimensional, ${\bf z}\equiv ({\bf x}, v_\parallel, \mu)$ representing position, the parallel velocity and the “magnetic moment”. The particle distribution function is written as $f=f_M+f_G+\delta f_P$, representing the Maxwellian background, an interpolation of data on a given Eulerian “grid” , and where $\delta f_P \equiv \sum \omega_i \delta({\bf z}-{\bf z}_i)$ represents the Lagragian “particles” each with weight $\omega_i$. At every time step, a small fraction $\alpha \ll 1$ of the particle distribution function is converted to the “grid data”, i.e. $f_G^{n+1}$ $=$ $f_G^n$ $+$ $\alpha f_P^n$, $f_P^{n+1}$ $=$ $(1-\alpha) f_P^n$ $+$ $\partial f_P/\partial t$, and $\omega_i^{n+1}$ $=$ $(1-\alpha) \omega_i^n$ $+$ $d\omega/dt$. The time evolution is described by the generalized Boltzmann equation, $\partial f / \partial t + {\bf \dot z} \cdot \partial f / \partial {\bf z} = C(f) + S(f)$, where the non-linear, Coulomb collision operator, $C(f)$, and the sources/sinks, $S(f)$, are evaluated on the phase-space grid.
The phase-space grid contains the slow evolution of $\delta f$, thereby mitigating the “growing-weight” issue, which is common to conventional $\delta f$ methods. The figure (click to enlarge) shows the square mean of particle weights, on the velocity grid, with two different $\alpha$'s; reduction in particle noise by factor of 4 is achieved with $\alpha = 10^{-3}$.
The Lagrangian particles allow efficient scalability on leadership-class computers, while a significant $f_0 \equiv f_M + f_G$ fraction residing on the phase-space grid minimizes the particle noise without demanding too much compute memory. Installed and utilized in XGC1 [5], the new method will speed up the ITER-critical, kinetic study of tokamak edge plasmas, allowing investigation of “blobby” turbulence, the pedestal height and width, the H-mode transition, and the divertor heat-flux width.
The world's largest-ever tokamak presently under constructing in France, namely ITER [1], may have to rely on self-generated intrinsic rotation, rather than externally produced rotation, for controlling both the macroscopic stability and reducing turbulent transport. A critical question is: what level of intrinsic rotation can be achieved? Predicting intrinsic-rotation profile structures of tokamak experiments present a great challenge, and also a great opportunity to test our understanding of turbulence-driving intrinsic rotation.
Recently, quantitatively good agreement between first-principles-based model predictions and high-quality experimental measurements of the intrinsic ion-rotation has been obtained for the first time in highly non-trivial, and relevant, configurations [2,3,4]. This allows verification and validation of the theoretical models for: turbulence-driving intrinsic rotation, the $k_\parallel$-symmetry breaking required for turbulence-driven residual stress; and global, gyro-kinetic (GK) simulation models for calculating momentum transport.
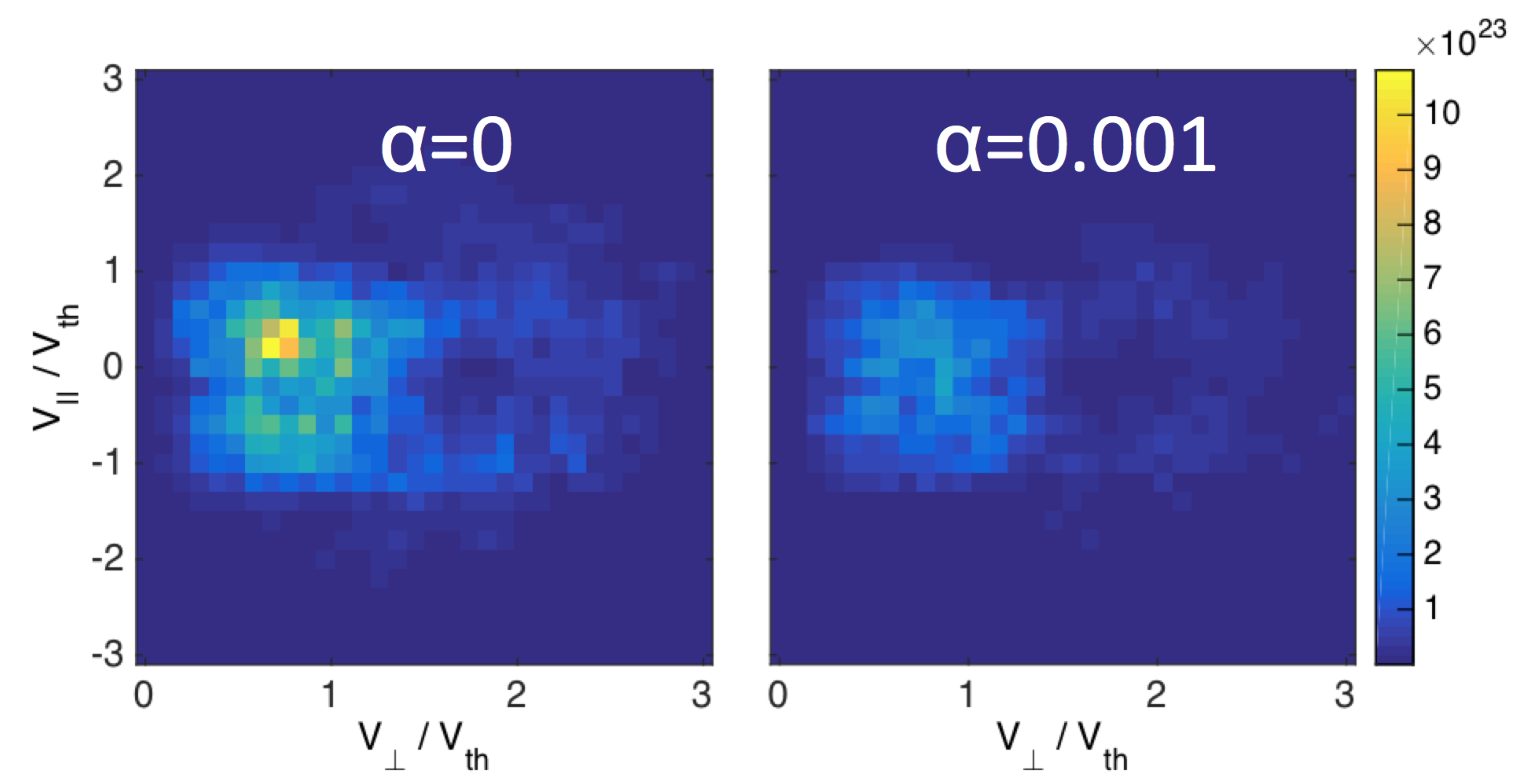
Nonlinear, global, gyro-kinetic simulations of DIII-D, electron cyclotron heated (ECH) plasmas indicate a substantial ion-temperature-gradient (ITG), fluctuation-induced, non-diffusive momentum-flux, generated around a peaked, intrinsic, toroidal rotation profile. The figure shows the simulated, turbulence-driven residual-stress, which displays a dipolar structure that produces the hollow rotation profile (top); and the predicted intrinsic rotation in comparison with the experimentally measured, main ion toroidal rotation. Both turbulence intensity gradient and zonal-flow, ${\bf E}\times{\bf B}$ shear are identified as major contributors to the generation of the $k_\parallel$-asymmetry needed for the residual stress generation [3,4]. By balancing the residual stress and the momentum diffusion, a self-organized, steady-state rotation profile is calculated. The radial structure of residual stress profile and associated intrinsic rotation gradient are shown to have a complicated dependence on multiple physics parameters, including turbulence type, $q$-profile structure, and collisionality. Interesting results obtained include the intrinsic rotation reversal induced by the change of type of underlying turbulence in flat-$q$ profile regimes and by change in $q$-profile from weak to normal shear. Simulations for this research were carried out by the Gyrokinetic Tokamak Simulation (GTS) code [5,6].
Astrophysical shock waves play diverse roles; including energizing cosmic rays in the blast waves of astrophysical explosions, and generating primordial magnetic fields during the formation of galaxies and clusters [?]. Inter-particle collisions are too weak to sustain shocks in these high-temperature, low-density astrophysical plasmas. Instead, plasma instabilities such as the Weibel [?] instability have been proposed to dynamically generate turbulent electric and magnetic fields in the shock front, which provides the mechanism for shock formation.
Recent experiments conducted on the OMEGA EP laser facility [?] at the University of Rochester Laboratory for Laser Energetics, have identified for the first time a long-predicted [?] “Weibel” or filamentation or instability between counter-streaming plasmas, which has been proposed to be a key ingredient in astrophysical shock waves. The observations are corroborated by analytic theory [?] and by massively parallel particle-in-cell simulations [?].
Due to the high-energy conditions, the interaction between the plasma plumes is relatively collisionless; the plumes are free to interpenetrate one another, thereby establishing highly non-Maxwellian, supersonic, counter-streaming ion flow conditions. The Weibel instability grows by tapping the free-energy in these non-Maxwellian features and produces characteristic magnetized filaments parallel to the flows. The electromagnetic fields in these filaments were observed in proton radiographs, using a proton beam driven by an additional high-intensity short-pulse laser. The instability is identified as an ion-driven Weibel instability through agreement with analytic theory. Particle-in-cell simulations [?] conducted on the Titan XK7 supercomputer [?] at ORNL, initialized with the relevant counter-streaming flow profiles, reproduce the growth rates and characteristic scales of this instability.
Plasmas in tokamaks (azimuthally-symmetric, magnetic-confinement devices) have been observed [1] to rotate spontaneously about their axis of symmetry, without the application of torque. This unexpected behavior could be very beneficial for the fusion program, since rotation helps to stabilize the plasma [2], but only small amounts of torque injection will be possible in any eventual reactor.
Both analytical calculations [3] and simulations with the XGC1 code [4] have identified a mechanism for this so-called “intrinsic” rotation near the plasma edge. As sketched in the figure (click to enlarge), ion drift orbits interact with plasma turbulence to cause the plasma to begin to rotate toroidally. Further inside the plasma, as the rotation profiles are often peaked, the angular frequency changes with radius, even when no torque is applied. The mechanism for this mysterious peaking is under ongoing investigation with the GTS code [5], which has numerically demonstrated the turbulent generation of such rotation peaking and found it to depend strongly on the pitch of the magnetic field and its radial variation, thus on the plasma current and its radial gradient [5].
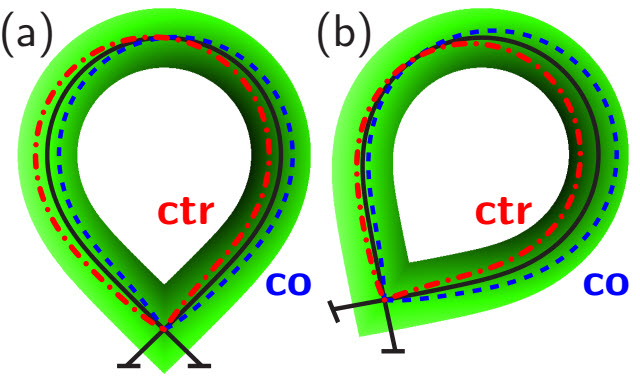
Two general transport mechanisms allow plasma to escape from magnetic-confinement devices such as tokamaks and stellarators: “neoclassical transport”, caused by collisions of the plasma particles with each other; and “turbulent transport”, caused by small-scale, turbulent fluctuations in, for example, the electric and magnetic fields. Turbulent transport is expected to be dominant over neoclassical transport in tokamaks, as well as in modern, neoclassically optimized stellarator designs [1]; finding experimental designs with appreciably-reduced levels of turbulent transport would greatly improve the performance of future fusion reactors.
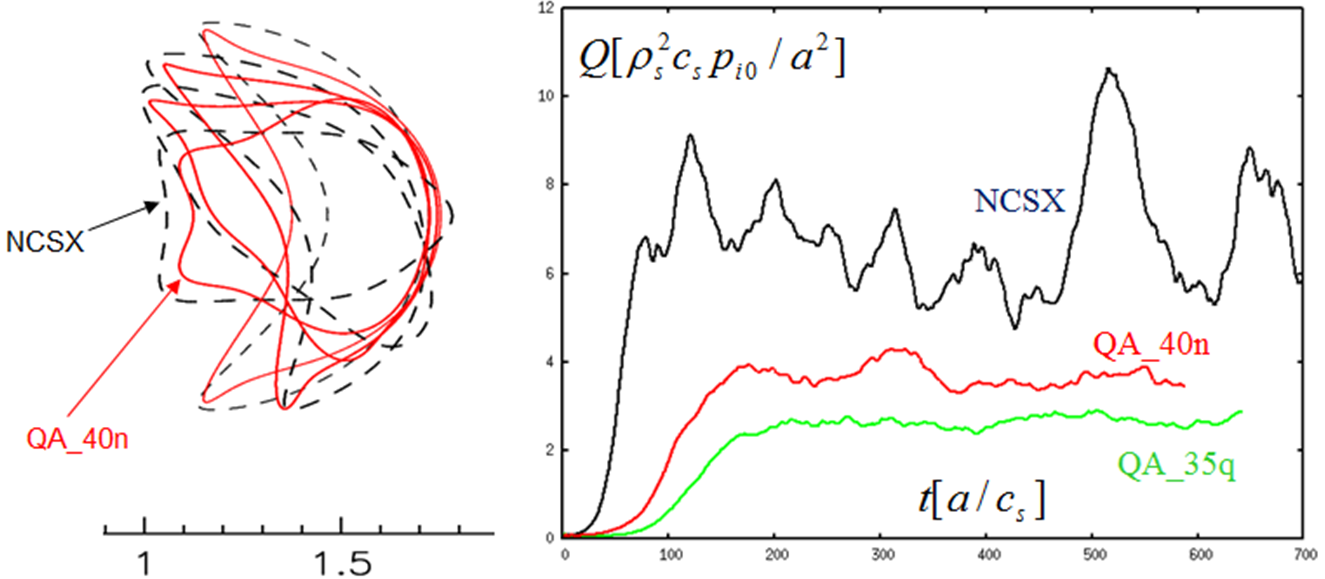
The recent advent of two powerful numerical tools, namely (i) gyrokinetic codes for turbulence simulation, such as GENE [2,3], and (ii) configuration optimization codes for both stellarators and tokamaks, such as STELLOPT [4], have for the first time allowed [5,6] existing stellarator- and tokamak-configuration designs to be optimized towards reduced turbulent transport. For example, the National Compact Stellarator eXperiment (NCSX) configuration design [7] was evolved, as shown in the figure (click to enlarge), to a configuration with significantly reduced turbulent heat-flux, $Q$, as calculated with GENE [5,6] simulations (as shown). Similar optimization calculations have similarly reduced turbulent-transport in tokamak configurations [8].
P.O. Box 451
Princeton, NJ 08543-0451 U.S.A
Tel: (609) 243-2000
