Energetic particle (EP) research is key for understanding the “burning plasma” (BP) performance; sustained burning, i.e., heating the plasma and compensating for energy loss due to transport processes, is crucial for fusion power stations. PPPL has played a leading role in EP research since its initiation in the 1980s, and reliable predictions can be made for the performance of future BP fusion devices. The work on EP research in Theory Department has several parts.
Linear and Nonlinear Instabilities of Waves Linear and nonlinear instabilities of waves, primarily Alfvénic waves, that are influenced strongly by the presence of energetic particles. Referred to as “kinetic magnetohydrodynamics”, this is strongly synergistic with the “Scientific Discovery though Advanced Computing” (SciDAC) “Center for Nonlinear Simulation of Energetic Particles in Burning Plasmas” (CSEP), which is led by PPPL, in partnership with multiple institutions over recent years. The M3D-K simulation code, which couples a kinetic description of energetic particles within an magnetohydrodynamic (MHD) framework, is a critical tool of CSEP research.
Transport of Energetic Particles The second part of EP research in the Department focuses on the transport properties of the energetic particles in the presence of instabilities and uses a combination of analytical approaches, such as quasilinear theory and numerical particle orbit studies. The self-consistent effects of energetic particles on plasma confinement are studied using the versatile, hybrid code HYM, which employs a fluid description of electrons and a fully kinetic description of ions. Both types of studies are strongly coupled to experiments, e.g. NSTX and DIII-D, for verification and validation. The EP group is an integral part of the PPPL EP Science Focus Group led by Dr. Gorelenkov.
Runaway Electrons The third part of EP research focuses on “runaway electron” physics. Electrons can be continuously accelerated by an electric field if it is stronger than the collisional drag from other particles. The prediction and mitigation of runaway electrons (REs) is one of the most critical challenges faced by ITER. According to present tokamak experimental results and theoretical models, it is expected that in a typical unmitigated disruption in ITER, a large fraction of the original plasma current will be converted to RE current (up to 10 MA), with RE energy about 10-20 MeV. Unfortunately, this localized RE beam, if unmitigated, might hit the wall with up to 160 MJ energy, with the potential to cause serious damage. Localized burn holes from REs have been observed on TFTR, JET and other experiments, and are projected to be far worse on ITER if they occur. In order for ITER to achieve its mission, avoidance and mitigation of REs is essential. These so-called runaway electrons can gain energy up to 10MeV in tokamak disruptions, and can also be formed under various scenarios; including solar flares and thunderstorms. In tokamaks with large equilibrium currents (such as ITER), the potential damage to the device is of programmatic importance. An important aspect of this research is the runaway electron “avalanche”, which comes from a large-angle scattering collision between an energetic-runaway electron and a relatively-low- energy, thermal electron, which can cause exponential growth. For highly-relativistic runaway electrons, the emitted radiation becomes substantial, including synchrotron radiation, bremsstrahlung radiation, and Cerenkov radiation.
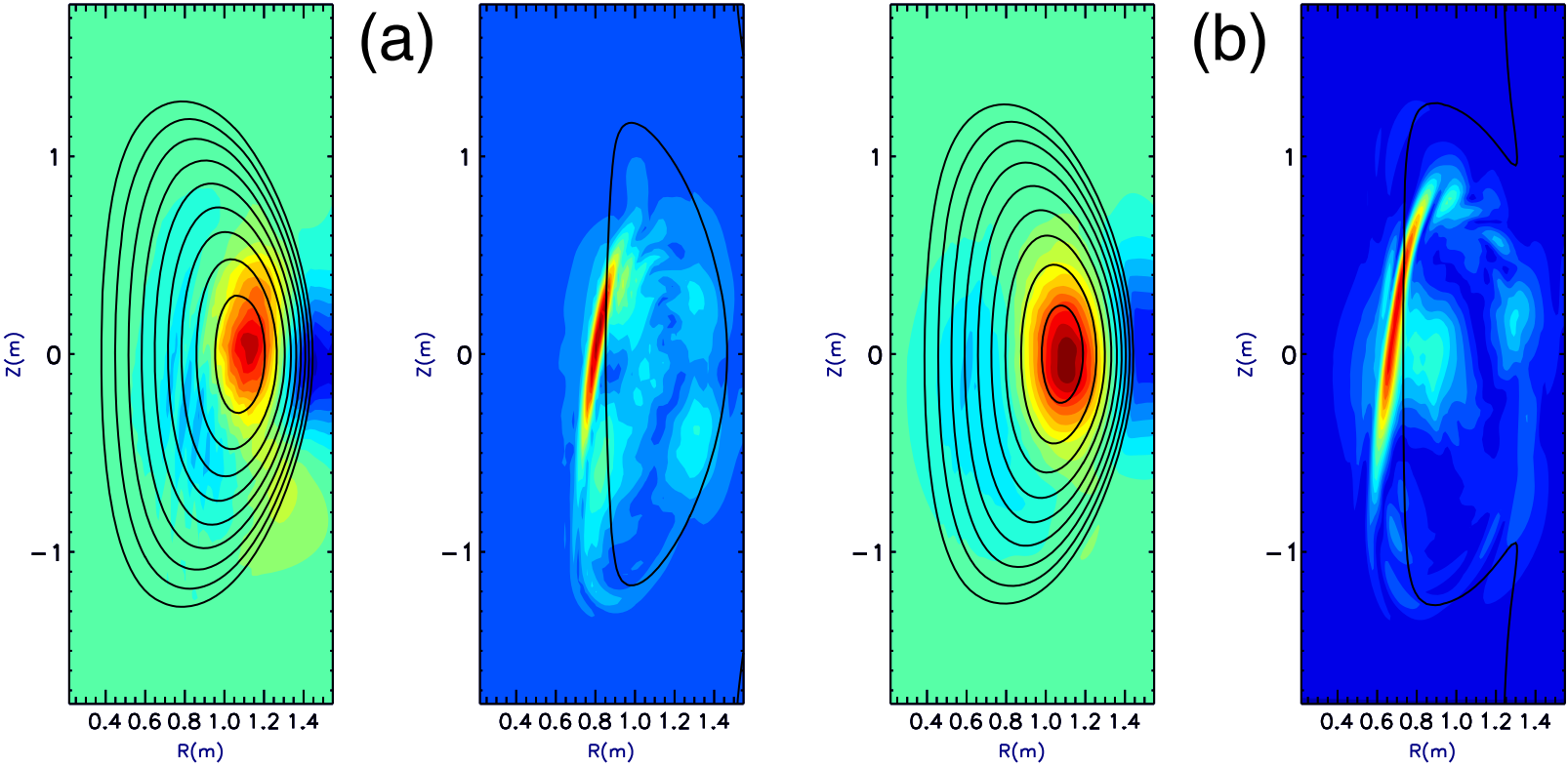
Experimental observations from the National Spherical Torus Experiment (NSTX) have linked strong activity of global (GAEs) and compressional (CAEs) Alfvén eigenmodes to a flattening of the electron-temperature, $T_e$, profile in beam-heated plasmas [1]. Previous theoretical studies [2] attributed this to enhanced electron-transport; however, a large number of unstable modes (>15), with relatively large amplitudes, was needed to explain the observed transport. A new, energy-channeling mechanism is proposed [3] that explains the lower heating-efficiency.
Simulations of neutral-beam-driven CAEs in NSTX discharge #141398 have been performed using the HYM [4] code; a three-dimensional, “hybrid”, nonlinear, global stability code, which treats the beam ions using “full-orbit”, $\delta f$, particle simulations, and treats the background plasma as a resistive, magnetohydrodynamic (MHD) fluid. These show unstable CAEs for a range of toroidal mode numbers, which “couple” to kinetic Alfvén waves (KAW) on the high-field side at the Alfvén resonance location (see figure, click to enlarge). The CAEs channel the energy of the beam ions from the injection region (near the magnetic axis) to the location of the resonant-mode conversion (at the edge of the beam-density profile). The CAE instability saturates nonlinearly because of particle trapping; and a large fraction of the beam energy can be transferred to unstable CAEs and be absorbed at the resonant location; with the absorption rate scaling strongly with beam power. The energy flux from the CAE to the KAW, and dissipation at the resonance location, can have a direct effect on $T_e$, with changes in core up to several hundred eV. The energy-channeling mechanism is generic: it applies to other toroidal devices as well as NSTX, where the CAEs are unstable.
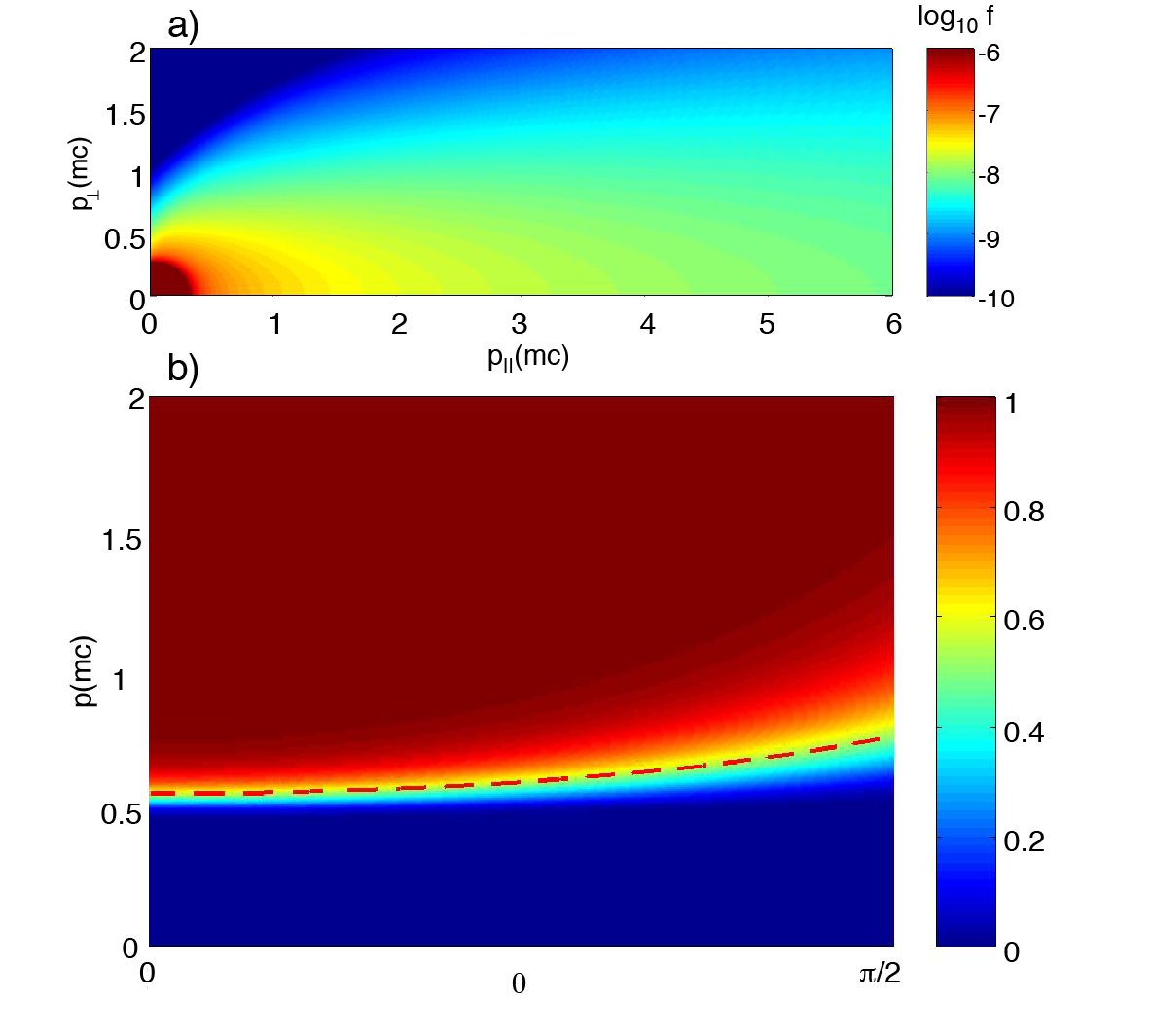
Under an external, electric field, a superthermal electron in plasma can be accelerated to very high energy [1]. So-called “runaway” electrons, if left unchecked, could severely damage the plasma-facing components on any tokamak as large as ITER [2] during an off-normal, “disruption” event; potentially taking the device out of operation for months! A theoretical understanding of the generation-mechanisms and dynamics of runaway electrons is, understandably, a critical part of fusion research. One goal of the research is to understand how the energy gained from acceleration caused by the electric field is countered by losses from radiation, collisional damping, and transport [3]; thereby forming a runaway electron tail, as shown in the figure a) (click to enlarge).
The dynamics of runaway electrons (in momentum space) can be described using a Stochastic Differential Equation (SDE) [4], where the randomness mainly comes from the pitch-angle scattering; however, SDEs are usually difficult to solve analytically, and expensive to simulate computationally. To understand the momentum-space structure of runaway electrons, we have [5] implemented an adjoint method [6] to calculate two important functions, namely the Runaway Probability Function (RPF), and the Expected Loss Time (ELT). The adjoint method can be regarded as a more-computationally-efficient, “backward” method; as compared to so-called “forward” methods such as the Monte-Carlo method of solving SDEs, and solving the time-dependent Fokker-Planck equation. As shown in figure b), the RPF clearly shows the “separatrix” between the runaway and the slowing-down regions in momentum space. The adjoint method can also be applied to study the runaway-electron “avalanche”; and can calculate both the critical electric-field and the growth rate for the avalanche.
Alfvén modes are fundamental oscillations ubiquitously observed in magnetized plasmas [1], which can extract energy from energetic-ion populations; leading to severe energy losses [2,3]. Interacting with fast ions, Alfvén waves can evolve nonlinearly to two distinct, and extreme, regimes: a nearly-constant-amplitude excitation with fixed frequency, or a coherent oscillation that “chirps” with frequency on timescales much shorter than plasma equilibrium timescales [4]. Chirping instabilities can be a harmful, convective mechanism of fast-ion losses; and can be prodromic of even worse, like the “avalanches” observed in NSTX [5].
Chirping onset was studied using the theory of driven, kinetic instabilities with dissipation [6], which was extended to account for multiple resonant-surfaces and realistic mode-structures.
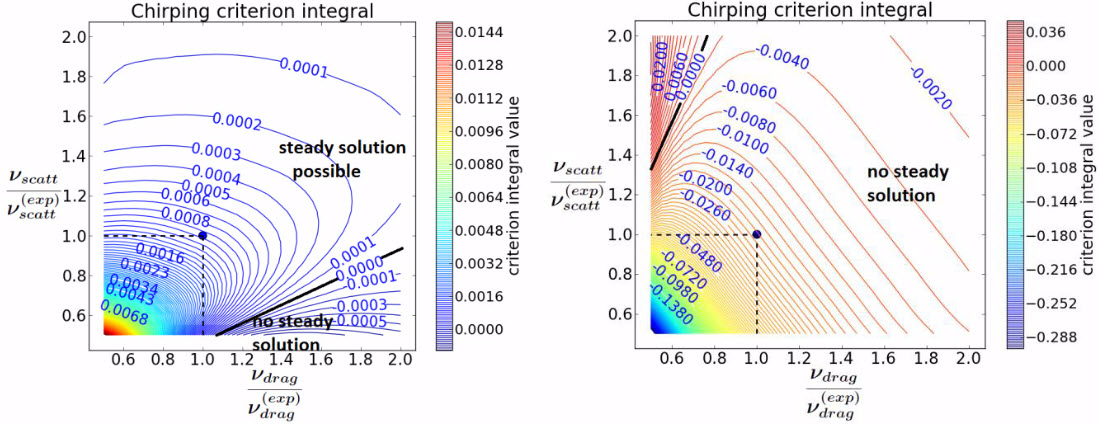
A “chirping” criterion was derived [7] that involves fast-particle-velocity drag, $\nu_{drag}$, and pitch-angle scattering, $\nu_{scatt}$; and which agrees with observations in different tokamaks, as reported by Dr. V.N. Duarte at the 2016 Sherwood Conference [7].
Coulomb collisions alone are not sufficient to explain experimental observations: micro-turbulence was introduced into the model, contributing an important diffusive mechanism responsible for fast-particle de-correlation from the coherent structures that support chirping.
The figure (click to enlarge) shows scans of the predicted criterion, calculated using NOVA-K [8], for a mode in DIII-D that starts chirping as the fast-ion interaction with the turbulence substantially decreases.
Consistent with theory, the wave transitions from fixed-frequency to chirping in the experiment only after a substantial drop of fast-ion particle diffusivity.
[Collaboration between PPPL, U. São Paulo, U. Texas (Austin), U. California (Irvine) and General Atomics.]
Some of the recent notable progress in the area of energetic particle (EP) research includes two activities. The first, lead by Dr. N.N. Gorelenkov together with Dr. S.D. Pinches from the ITER organization and Dr. K. Toi of the National Institute for Fusion Sciences, Japan, was to prepare a review for the journal Nuclear Fusion titled “Energetic particles in fusion in preparation for burning plasma experiments” [1]. The review is timely as the fusion community readies itself for future burning plasma operations on ITER, and it was selected for the inclusion in the exclusive Nuclear Fusion 2014 highlights collection for “its outstanding quality and valuable contribution to the fusion community”.
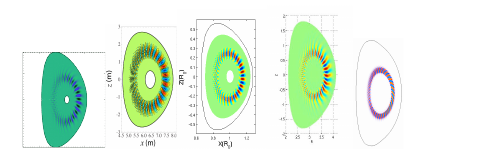
The second, high-impact research example in this area is the “FY2014 Fusion Energy Sciences, Theory & Simulation Performance Target” [2] milestone led by PPPL, which included several institutions. It was formulated as “Understanding alpha particle confinement in ITER”, the world's first burning plasma experiment, with the goals: to determine the linear instability trends and thresholds of energetic-particle-driven, shear Alfvén eigenmodes in ITER for a range of parameters and profiles using a set of complementary simulation models (gyrokinetic, hybrid, and gyrofluid); and to carry out initial, nonlinear simulations to assess the effects of the unstable modes on energetic particle transport. This milestone is one of the first comparisons between several initial-value codes, including GEM (Y. Chen, U. Colorado), GTC (Z. Lin, UCI), TAEFL (D. Spong, ORNL), GYRO (R. Waltz) and M3D (G.-Y. Fu), and the linear kinetic stability code NOVA-K (N.N. Gorelenkov, PPPL). The figure shows the comparison of five mentioned initial value code, which show almost the same structure of the toroidal Alfvén eigenmodes (TAE) mode in ITER.