Basic plasma theory is the exploratory study of elementary plasma phenomena and new approaches to modeling plasmas analytically and computationally. Advances in basic theory are converted into practical applications across a wide range of plasma physics research.
Short laser pulses are useful because they can resolve transient, atomic and sub-atomic phenomena, and because they can reach ultra-high intensities. The quest for higher laser intensity and shorter pulse duration has stimulated rich study in both solid-state lasers and plasma compressors, such as backward Raman amplifiers [1,2]. The current state-of-the-art technique is represented by chirped pulse amplification [3], which can produce over $10^{14}W$ laser pulses. Further increasing pulse intensity using conventional techniques is difficult. Instead, Raman amplification of laser beams using plasma promises a breakthrough by the use of much smaller amplifying media.
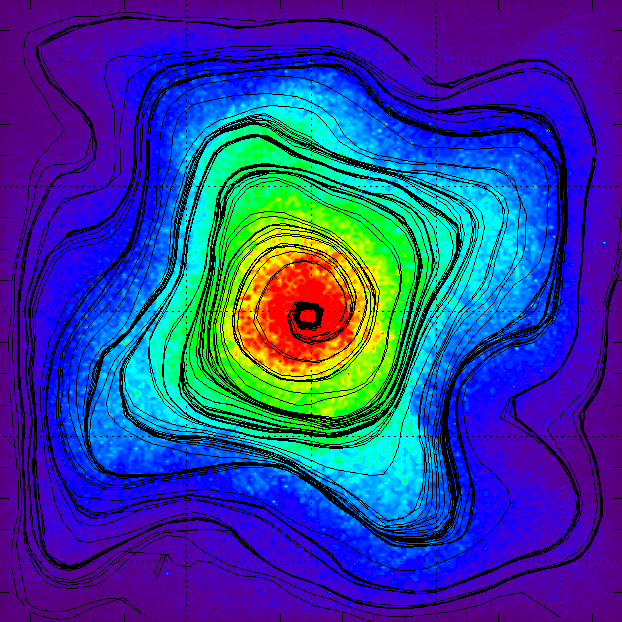
Qu, Barth and Fisch [4] have proposed a novel configuration of backward Raman amplifiers by replacing the traditional counter-propagating laser seed with a plasma wave seed. This avoids issues [5] in preparing and synchronizing a frequency-shifted laser seed. They find a condition under which the plasma wave seed strictly produces the same output pulse as a counter-propagating laser seed. The advantageous, self-similar “attractor” solution can also be achieved in the longtime asymptotic limit, as shown by numerical particle-in-cell (PIC) simulations (as shown in figure, click to enlarge). Qu et al. prove that chirping the plasma wave wavelength can produce the same beneficial effects as chirping [6] the seed wave frequency.
The proposed plasma-wave-seeded Raman amplifier is comprised of an input laser pulse, called the “pump”, and a short plasma layer with a pre-existing plasma wave at one end. When the pump laser reaches the plasma wave, the Raman amplification is triggered, and this generates a counter-propagating “probe” pulse. The pump laser continuously deposits its energy into the wavefront of the probe pulse by parametrically interacting with plasma waves. The result is that almost all the pump energy is focused to the very front of the probe yielding an ultra-intense yet ultra-short laser pulse. The thermal threshold of conventional solid-state laser sources is overcome and ultra-high brilliance laser pulses are generated using the damageless property of plasmas. Full relativistic PIC simulations have shown that Raman amplifiers can generate a pulse with $~10^{18} W/cm^2$ intensity, which can reach peak intensities of $10^{25} -10^{29} W/cm^2$ after focusing.
Radio-frequency (RF) waves are critical not only for the heating and current drive in magnetically-confined plasmas, but also for diagnostics; however, the mathematical machinery for modeling these waves through traditional Vlasov-Maxwell theory in fusion plasmas remains antiquated. Dr. I.Y. Dodin et al. have introduced abstract mathematical methods that recognize rapid oscillations of wave fields as a distinct type of plasma dynamics with its own fundamental equations and symmetries [1].
The development of such modernized language for wave theory, originally pursued through fundamental studies of laser-plasma interactions at Princeton University funded by the National Nuclear Security Administration (NNSA) and the Defense Threat Reduction Agency (DTRA), can now be applied with particular benefit to RF applications in tokamaks, and in other magnetic fusion devices. For example, full-wave codes could make use of the manifestly-conservative nature that the wave equations have (modulo true, physical dissipation) in their fundamental representation. It may be possible to improve the accuracy of ray-tracing codes by including the effect of polarization-driven bending of ray trajectories [2,3]; and nonlinear wave-wave interactions can be described as ponderomotive effects on photons [4], as illustrated by the figure (click to enlarge).
We have found a new formulation of collisionless electromagnetic gyrokinetic theory with three novel features: (i) it is manifestly gauge invariant; (ii) the equations governing the electromagnetic field are hyperbolic in nature; and (iii) the gyrokinetic system of equations can be cast as an infinite-dimensional noncanonical Hamiltonian system [1]. \begin{eqnarray} \left[ {\cal F},{\cal G}\right] & = & \sum_{s=1}^{N_s} \int {\cal B}_{s}^{gy} \left( {\bf d}\frac{\delta {\cal F}}{\delta f_s} - 4 \pi e_s \frac{\delta {\cal F}}{\delta {\bf D}} \cdot d{\bf X}, {\bf d}\frac{\delta {\cal G}}{\delta f_s} - 4 \pi e_s \frac{\delta {\cal G}}{\delta {\bf D}} \cdot d{\bf X} \right) f_s \\ & + & 4 \pi c \int \left( \frac{\delta {\cal F}}{\delta {\bf D}} \cdot \nabla \times \frac{\delta {\cal G}}{\delta {\bf B}} - \frac{\delta {\cal G}}{\delta {\bf D}} \cdot \nabla \times \frac{\delta {\cal F}}{\delta {\bf B}} \right) d^3{\bf X}. \end{eqnarray} We have therefore succeeded in importing to gyrokinetics all of the qualitative mathematical structure contained in the “collisionless theory of everything”, which is embodied by the Vlasov-Maxwell equations. Interestingly, the new formulation supports light waves, but these propagate at the Alfvén speed instead of the speed of light. The culprit for this modification is the large effective dielectric constant in the gyrokinetic vacuum.
By leveraging the model's Hamiltonian form, we have derived an energy principle for assessing the stability of electromagnetic gyrokinetic equilibria. As a proof-of-principle calculation involving the energy principle, we have constructed the first rigorous proof that a gyrokinetic thermal equilibrium in a uniform background is stable. There is a growing need for reduced data motion and increased efficiency-to-solution in algorithms deployed on modern massively-parallel super computers. In light of this challenge, these new gyrokinetic equations offer an attractive alternative basis for large-scale gyrokinetic simulations. Due to the hyperbolic nature of the field equations, all dynamical variables in the theory can be advanced on a parallel computer in a manner that requires only nearest-neighbor, i.e. local, communication.
The fundamental theoretical framework of accelerator physics is based on the Courant-Snyder (CS) theory, a theoretical description of charged particle dynamics in an alternating-gradient quadrupole focusing lattice developed by Courant & Synder in 1958 [1]; however, the CS theory can only be applied to the ideal case of an uncoupled, quadrupole focusing lattices. In realistic accelerators, there also exist “bending” magnets, torsion of the design orbit (fiducial orbit), and skew-quadrupole components introduced intentionally or by misalignment. In certain applications, solenoidal magnets are also used. When these realistic components are considered, a new theory in a higher dimension is needed.
The generalized Courant-Snyder theory published this month [2] fulfills this much-needed role. The envelope function of the original CS theory is generalized into an envelope matrix, and the phase advance is generalized into a 4D sympletic rotation (also known as the $U(2)$ group). The envelope equation, transfer matrix, and the CS invariant of the original CS theory, all have their counterparts, with remarkably similar expressions, in the generalized theory. The generalization of the 1D envelope equation (also known as the Ermakov-Milne-Pinney equation in quantum mechanics) to higher dimensions will have broad applications in various branches of physics.
To accelerate and transport high-intensity beams, it is also critical to understand in what modes the beams can propagate quiescently through an alternating-gradient focusing channel. Until now, the only known class of exactly soluble modes of intense beam propagation including self-electric and self-magnetic field effects is the Kapchinskij-Vladimirskij (KV) distribution discovered in 1959. Using the generalized CS theory, and in particular the generalized envelope equation in higher dimension, a new class of propagation modes admitted by the nonlinear Vlasov-Maxwell equations was discovered after applying the Cholesky decomposition technique [3]. The newly discovered propagation modes enable a large increase in flexibility in the amount of beam control and steering capability. For example, the new modes allow the beam to “tumble” (rotate) in the transverse plane perpendicular to the propagation direction, which can be utilized as a beam smoothing technique for accelerator applications where smooth illumination is required, such as in the case of accelerators for heavy ion fusion and medical applications.