Nonlinear dynamical systems may be formally deterministic , in that if the initial conditions are known precisely then the state of a system can be predicted; however, the dynamical trajectories are highly sensitive to the initial conditions, so that small uncertainties can grow exponentially, a response popularly referred to as the butterfly effect, so that in practice deterministic systems can sometimes be treated using statistical methods that assume random behavior.
Nonlinear dynamical systems theory plays an important role in many areas of plasma dynamics; for example, error fields and three-dimensional shaping of the magnetic field can lead to magnetic field lines with chaotic trajectories, which degrade plasma confinement. The “good” magnetic surfaces required for plasma confinement break into resonance zones “magnetic islands”; and where the magnetic islands overlap, the magnetic field lines wander irregularly. Magnetic surfaces with irrational frequency disintegrate and develop the structure of a Cantor set, and are known as “cantori”, which provide partial barriers to phase-space transport. Shown in the figure (click to enlarge) as black dots in the Poincaré plot is a selection of cantori that restrict the radial transport of magnetic field lines, shown in green and red [Phys. Rev. E 74, 056203 (2006)].
Transport in both dissipative and Hamiltonian systems exhibit departures from normal diffusion, with the fine structure of phase space the primary origin of the anomaly: phase-space trajectories that visit “boundary layers” in the vicinity of islands display long-range correlations.
Anomalous transport is investigated [1,2] in the widely-used, discrete-time “standard map” [3], \begin{eqnarray} p_{n+1} &=& p_n - k \sin x_n,\\ x_{n+1} &=& x_{n} + p_{n+1}, \end{eqnarray} where $p$ and $x$ represent the momentum and position, and the subscript represents the discrete time. In spite of its simplicity, the standard map exhibits much of the complexity and canonical behavior of more-complicated dynamical models. The parameter $k$ represents a perturbation to a “integrable” dynamical flow: for $k=0$, the motion is trivial, $p_n = p_0$. For non-zero $k$, the dynamics depends sensitively on the initial conditions, and the motion can be irregular; but for $k < k_c$, where the critical perturbation is $k_c \simeq 0.9716...$ [4], the long-time excursion of $p$ is bounded by the existence of so-called, “good”, Kolmogorov-Arnold-Moser (KAM) surfaces [5,6].
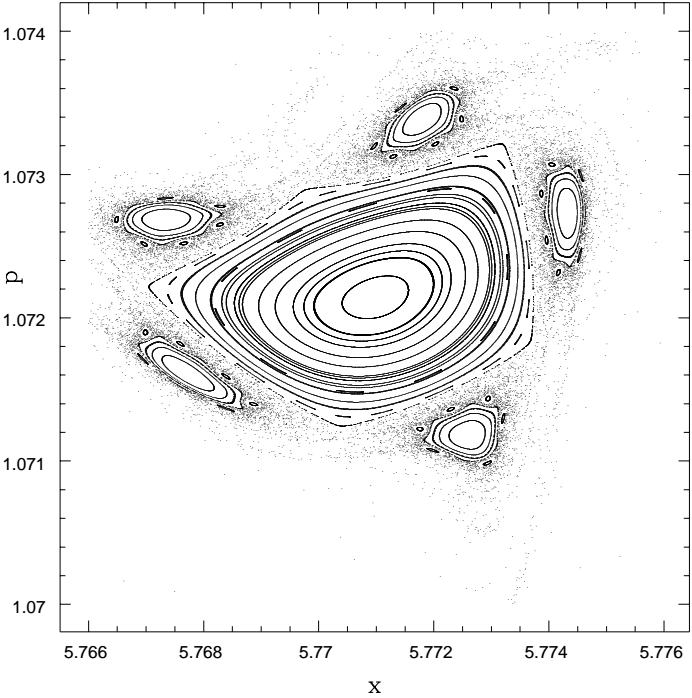
For $k > k_c$, $p$ can increase arbitrarily, and motion can sometimes appear to be diffusive; however, in the near-threshold case, the existence of very-long-time Lévy flights and large anomalies in the transport, i.e. $p^2 \sim t^\mu$ with $\mu \ne 1$, are shown to be associated with a new form of “multi-island” structure that causes orbit “sticking”. The largest effects in anomalous transport are due to the birth of new, “high-order” island chains; of which an example is shown in the figure (click to enlarge) for $k=1.62914292$, which also shows irregular (volume-filling, “random”) trajectories.
The modification of particle distributions by magnetohydrodynamic (MHD) modes is an important topic for magnetically confined plasmas. Low-amplitude modes are known to be capable of producing significant modification of injected neutral beam profiles, and the same can be expected for so-called “burning” plasmas for the $\alpha$-particle distributions.
In this work [1-4] we introduce a new method of determining domains of phase space in which good, so-called “KAM” surfaces do not exist; and which gives giving “exact” resonance locations and island widths.
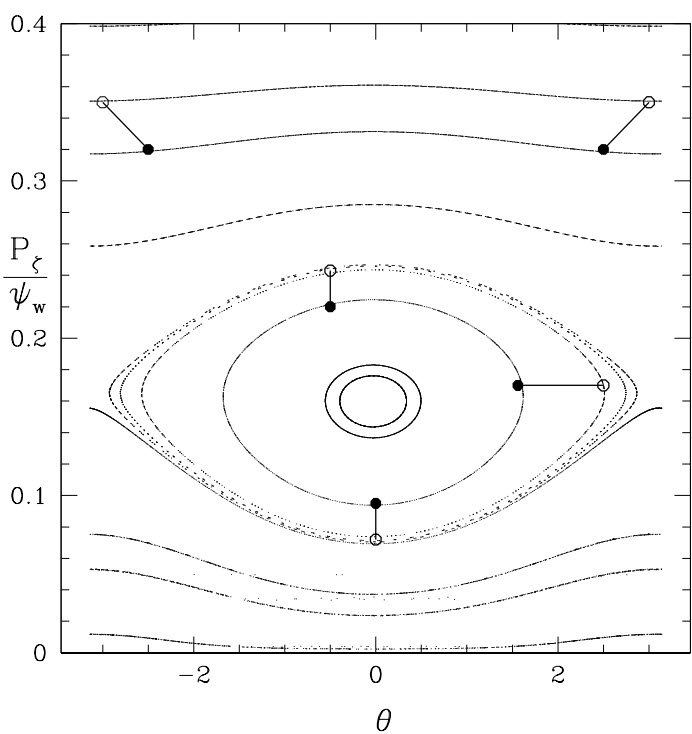
Consider following two, nearby dynamical trajectories in the $(\theta,P_\zeta)$ plane, where $(\theta,\zeta)$ describe the position and $(P_\theta,P_\zeta)$ describe the canonical momenta; and define the angle $\chi$ as the orientation of the vector joining them. If KAM surfaces exist, $\chi$ can change by at most an angle of $\pi$, due to their relative velocity in $\theta$; however, trajectories within an island rotate around each other, with $\chi$ increasing with the rotation about the island O-point, which increases with the size of the island.
This is illustrated in the figure (click to enlarge), which shows vectors between nearby points in the $(\theta,P_\zeta)$ plane on KAM surfaces and in a resonance. The angle $\chi$ rotates without bound in a stochastic domain (not shown). Thus, we determine the non-existence of KAM surfaces by examining nearby pairs of orbits, looking for where $\chi$ exceeds $\pi$.
The reversed-field pinche (RFP) class of magnetic confinement devices are more susceptible to non-linear effects and turbulence than tokamaks; and because experimental diagnostics accurately determine the magnetic field, which is generally non-integrable, RFPs are a perfect for testing theories of chaotic transport. We numerically model [1] the magnetic structure and the associated particle transport for the RFP experiment at the Consorzio RFX, Padova, Italy.
Particle transport in toroidal, plasma confinement devices is non-diffusive when magnetic chaos is present (see #highlight25 above); so a two-fluid, non-local, “Montroll” equation [2,3] is used to model the transport in RFX. Montroll equations describe stochastic, “jump” processes, with arbitrary distributions of jump lengths and waiting times, and is a generalization of a continuous-time, random walk. The required input information consists of a distribution of the Lévy flight times and distances.
We define a “flight” to be a trajectory with one sign of the “pitch”, $\lambda \equiv v_\parallel/v$, with $v_\parallel$ the particle velocity, ${\bf v}$, parallel to the magnetic field, ${\bf B}$; and describe the motion as a sum over flights. The probability has the general form $p(r',dr,dt)$, with $dr$ the distance moved across the “background”, equilibrium surfaces, $\psi$; and $dt$ is the flight time. The flight-time distribution is given by the pitch-angle scattering operator, $\lambda'$ $\equiv$ $\lambda (1-\nu dt)$ $\pm$ $\sqrt{(1 - \lambda ^2)\nu dt}$, where $\nu$ is the collision frequency. This gives a flight-time distribution of $\psi(t) = a(t_0 + t)^{-1.4}$.
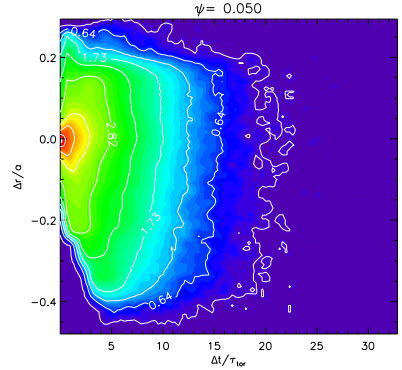
The flight-distance probability, $p(r',r-r',t-t')$, depends on the initial position and on the flight direction and duration; and describes the Lévy flights of the passing particles. An example is shown in the figure (click to enlarge). The asymmetry of this plot indicates the variation of the “degree-of-stochasticity” of the field. The probability vanishes for large distance and small time, and this reflects the causal nature of the propagation.
Toroidal magnetic fields are analogous to $1\frac{1}{2}$-dimensional Hamiltonian systems, and without a continuous symmetry such systems are generally have a fractal mix of (i) invariant flux (KAM) surfaces, (ii) cantori ($\equiv$ “broken” KAM surfaces) [1] (iii) unstable periodic orbits and their unstable manifolds, which constitute the stochastic sea, and (iv) stable periodic orbits and elliptic island chains. How do non-integrable, “chaotic” magnetic fields support temperature and density gradients where no flux surfaces exist?
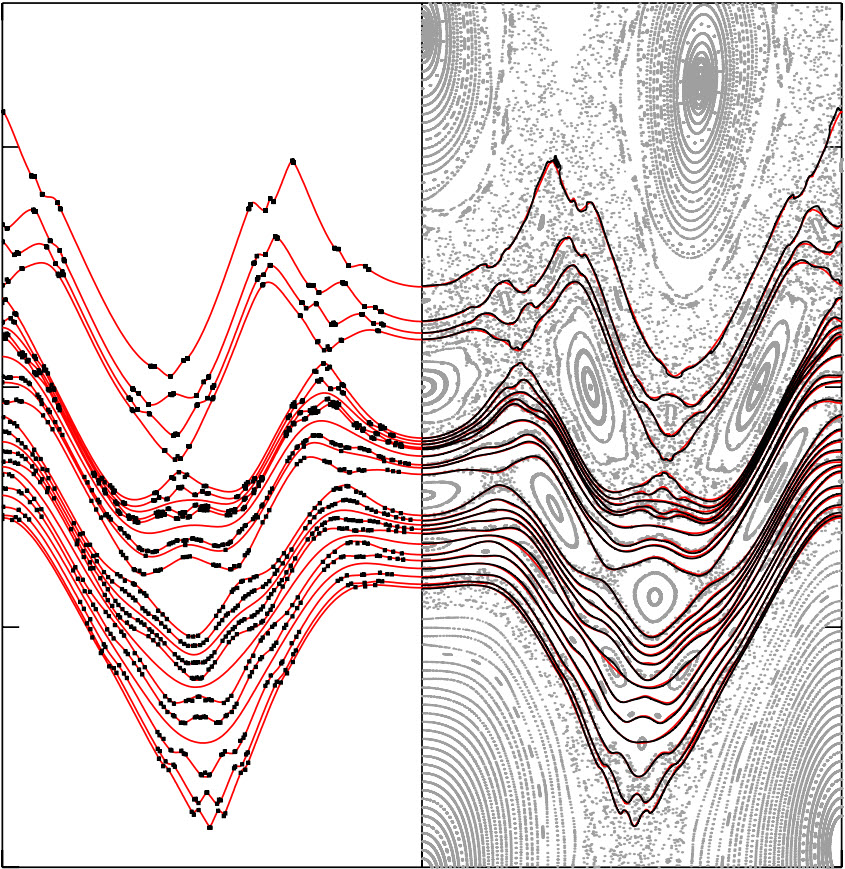
Dr. S.R. Hudson and Dr. J. Breslau [2] showed, by filling in the “holes” in the cantori using the mathematical construction of “ghost surfaces”, that temperature gradients will conform to the structures of the magnetic field that are nearly invariant under the fieldline dynamics. Ghost surfaces are defined using an “action-gradient flow”, $\partial {\cal C} / \partial \tau = - \partial {\cal S} / \partial {\cal C}$, where the action for magnetic fields, ${\bf B} = \nabla \times {\bf A}$, is ${\cal S}[{\cal C}] \equiv \int {\bf A} \cdot d{\bf l}$ and is considered to be a functional of an arbitrary “trial curve”, ${\cal C}$. Using an anisotropic-diffusion model for temperature transport, $\partial T / \partial t = \nabla \cdot ( \kappa_\parallel \nabla_\parallel T + \kappa_\perp \nabla_\perp T ) + (source)$, the enclosed figure (click to enlarge) shows [2] that the temperature adapts to the ghost surfaces, and that the radial temperature profile across chaotic fields is described [3] by \begin{eqnarray} \frac{dT}{ds} = \frac{c}{\kappa_\parallel \varphi + \kappa_\perp G}, \end{eqnarray} where $\varphi$ is related to the quadratic flux and $G$ is a geometric quantity, and $s$ is a radial coordinate. As $\kappa_\perp / \kappa_\parallel \rightarrow 0$, the temperature profile develops a fractal, “devil's staircase” structure (except that the temperature gradients are supported on the uncountable set of irrational KAM surfaces, rather than on a countable set.) Ghost-surfaces are intimately related [4,5] to the “quadratic-flux minimizing” surfaces introduced in [6].