This encompasses research from the sun to the heliopause, with particular emphasis on understanding the role of basic plasma processes such as reconnection, kinetic effects, wave-particle interactions, and turbulence throughout the heliosphere.
Topics of interest include: solar convection, solar flares, cornal mass ejections, heating of the solar wind, solar radio bursts, solar wind turbulence, particle acceleration in shocks, solar-wind magnetosphere coupling, plasma entry and transport in planetary plasma sheets, auroral phenomena, substorms, waves and transport in the inner magnetosphere, magnetosphere-ionosphere coupling, nonlinear dynamics in the heliosphere and space weather.
The theory of black-hole accretion is central to many areas of theoretical, computational, and observational astronomy. Not only does accretion power some of the phenomenologically richest electromagnetic sources in the Universe, but also black-hole accretion flows serve as excellent laboratories for the study of basic plasma dynamics and general relativity. The first step to understanding black-hole accretion flows is to determine why they accrete. What mechanism is responsible for the enhanced outward transport of angular momentum and the consequent infall of mass? Two decades worth of magnetohydrodynamic (MHD) simulations and theory suggest that the magnetorotational instability (MRI) [1] simultaneously enables mass accretion by efficiently transporting angular momentum outwards and amplifies the magnetic field to near equipartition strengths. While useful, the MHD description is remarkably incomplete; in fact, it is strictly inapplicable in many accreting systems, most notably that onto Sagittarius A* (Sgr A*), a bright, compact astronomical radio source at the center of the Milky Way [2], in which the Coulomb mean free path between collisions is much larger than the characteristic scale of the flow.
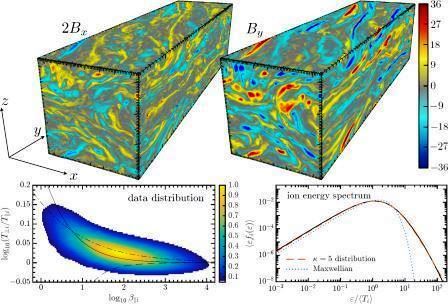
The work featured here provides, for the first time, ab initio evidence for the existence and efficacy of magnetorotational turbulence and dynamo in a collisionless plasma [3]. The key feature is that the MRI, by virtue of producing correlations in turbulent fluctuations and thereby amplifying the magnetic field (top row of figure), drives the plasma distribution function away from the thermodynamic equilibrium (figure bottom left, click to enlarge), yielding both macroscopic and microscopic consequences. On large scales, significant Maxwell and Reynolds stresses are accompanied by comparable viscous stresses produced by field-aligned temperature anisotropies. On small scales, such temperature anisotropies drive Larmor-scale instabilities that are responsible for scattering and trapping particles [4], thereby endowing the otherwise collisionless plasma with an effective viscosity. Other notable results include the observation and characterization of Alfvén-wave and kinetic-Alfvén-wave cascades in MRI turbulence and non-thermal particle acceleration (figure bottom right, click to enlarge). These results were obtained using the hybrid-kinetic particle-in-cell code, Pegasus, developed at Princeton University by M. Kunz, J. Stone & X. Bai [5].
Impulsive phenomena, such as magnetospheric substorms, and solar and stellar flares, are known to be driven by fast magnetic reconnection events [1], which rapidly transform magnetic energy to plasma particle energy. Fast magnetic reconnection would normally be impossible for reconnecting current sheets that are highly elongated, since they severely constrain the velocity of the plasma entering the reconnection layer. However, it has been known since the 1980s that such sheets are subject to a violent instability, known as the plasmoid instability [2]. A thorough knowledge of the properties of the plasmoid instability is therefore essential in understanding many important questions, such as the onset of fast reconnection.
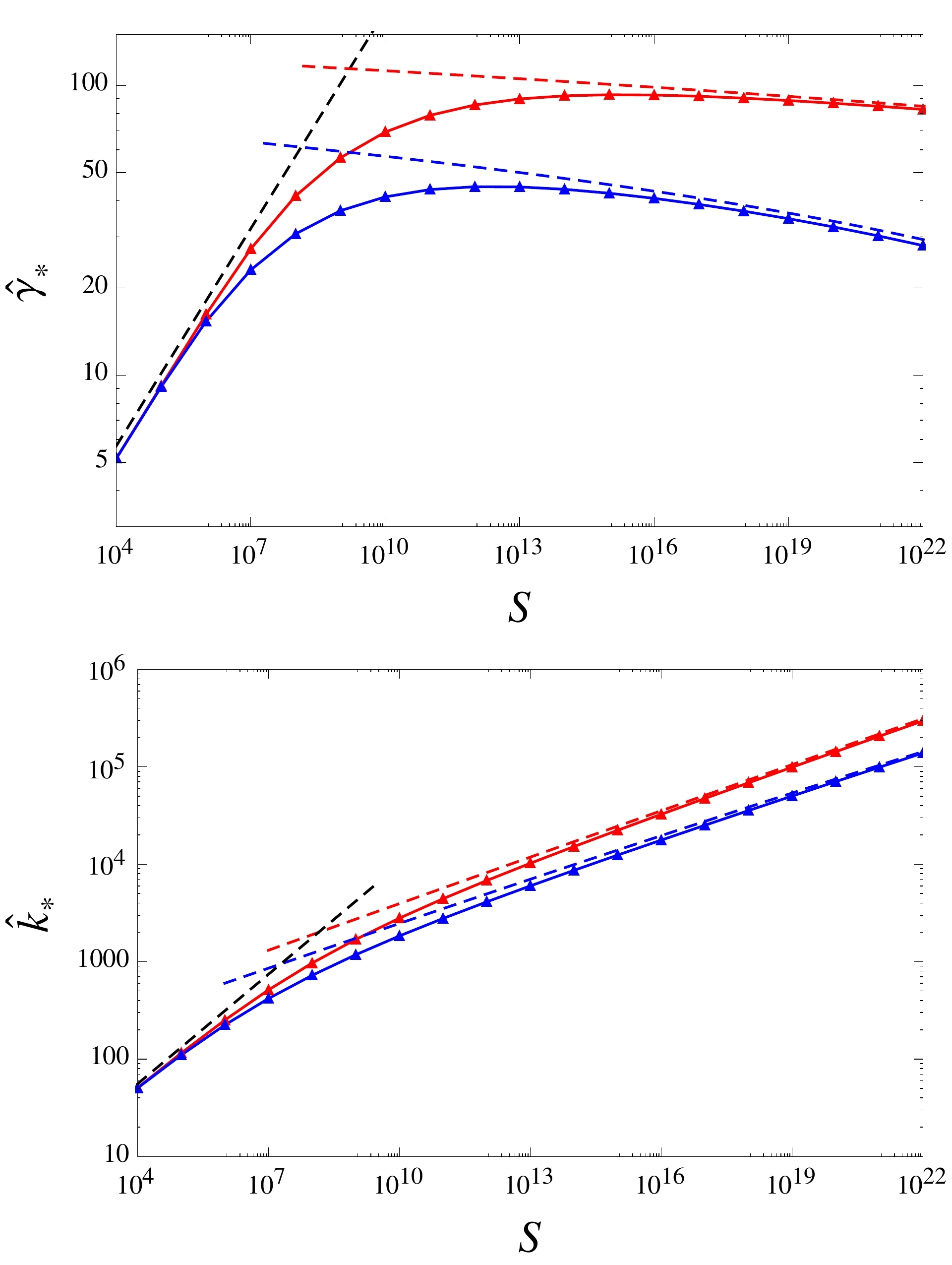
Recently, Dr. L. Comisso, Dr. M. Lingam et al. formulated a general theory of the onset and development of the plasmoid instability by means of a principle of least time [3]. This approach has lead to completely new results, which have shown that previously obtained power laws are insufficient to capture the correct properties of the plasmoid instability. Specifically, the scaling relations for the final aspect ratio, transition time to rapid onset, growth rate, and number of plasmoids have been shown to be proportional to $S^{\alpha} \tau^{\beta} \left[\ln f(S,\tau,{\hat w}_0)\right]^\sigma$, where $S$ is the Lundquist number, ${\hat w}_0$ is the initial perturbation amplitude, and $1/\tau$ is the characteristic rate of current sheet evolution.
The figures illustrate the dependence of the growth rate ${{\hat \gamma }_*}$ and the wavenumber ${{\hat k}_*}$ as a function of the Lundquist number $S$, for different perturbation amplitudes. The black dashed lines represent the earlier scalings, which are not applicable for large-$S$ plasmas, while the solid curves represent the accurate results obtained with the new theoretical approach [3].
Could a large-scale magnetic field grow out of turbulence and be sustained despite the presence of dissipation? What are the minimum ingredients for large-scale dynamo growth?
Recently, Dr. Ebrahimi & Dr. Blackman [1] have identified the minimum conditions needed for large-scale field growth. Though quasilinear calculations and numerical simulations, they have shown that the combination of imposed non-axisymmetric fluctuations, even if not helical, and differential rotation (or linear shear in the Cartesian approximation) of the fluctuating field is sufficient to source the electromotive force and generate a large scale magnetic field.
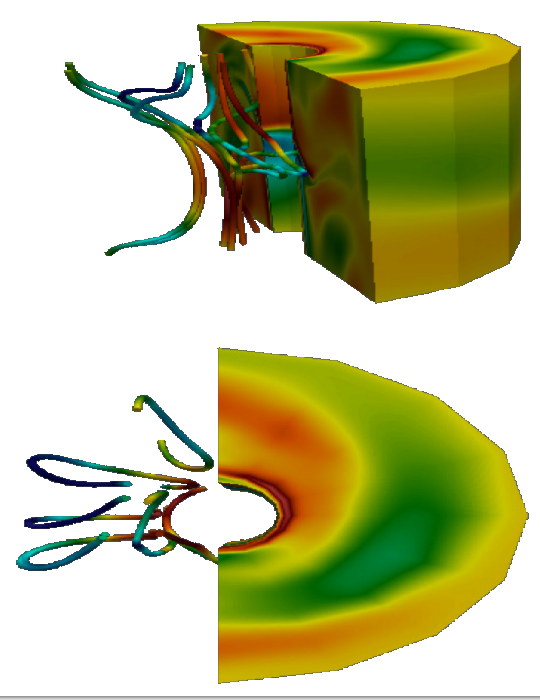
The figure (click to enlarge) shows fieldline visualizations in three-dimensional, non-linear, magnetorotational instability (MRI) simulations: the fieldlines are stretched and twisted to generate a large-scale, toroidal field. Dr. Ebrahimi and Dr. Bhat [2] perform direct numerical simulations to study MRI dynamo in both global cylindrical geometry and in a local “shearing” box. Studies of field generation in both flow-dominated astrophysical and magnetically-dominated, laboratory systems is one of the major research interests of this group [3].
Drs. P. Porazik & J. Johnson are currently advancing a gyrokinetic model for dipole geometry, which approximates the magnetic field of the inner magnetosphere [1]. This model exploits gyro-symmetry, the symmetry of the motion of a charged particle in a magnetic field associated with its relatively fast gyration, to provide a simplified kinetic description that essentially follows the self-consistent motion of charged rings in electromagnetic fields and has been applied to study Ultra Low Frequency (ULF) waves that are generated through drift-bounce resonance with energetic particles, such as the drift-compressional mode displayed in the figure above (click to enlarge). The model does not employ a bounce averaged distribution and, rather than assuming a quasi-equilibrium, allows for pressure imbalance, launching of magnetohydrodynamic (MHD) waves, and self-consistent evolution of the plasma population in the presence of MHD waves that cause radial transport. The formalism follows guiding centers that respond to the large-scale spatio-temporal fields and a transform that responds to small-scale spatio-temporal fields.
The simplification is that the guiding center equations depend only on slowly varying quantities and the interaction of the waves with the particles is contained in a single scalar equation for the gauge (coordinate transformation). This approach can potentially be coupled to our finite element wave model by separating the transport and wave timescales. Moreover, the formalism also allows an extension to higher frequency, for a self-consistent description of ElectroMagnetic Ion-Cyclotron waves (EMIC) and whistler waves as has currently been performed at PPPL.
Plasma waves are primarily observable in space. Understanding the physical processes is fundamental for understanding the plasmasphere, magnetosphere, and space weather. To investigate wave propagation in arbitrary, planetary magnetospheres, we developed a two-dimensional, finite-element, “full-wave” code, FWRD [1,2]. The boundary shapes, plasma-density profiles and the magnetic-field configurations are readily adapted, and the resolution can be “packed” where required. FWRD solves the “cold-plasma”, wave equations in two-dimensions: assuming a time dependence $\exp(−i \omega t)$, the linear and cold-plasma wave equation is \begin{eqnarray} \nabla \times \nabla \times {\bf E} - \frac{\omega^2}{c^2} \epsilon \cdot {\bf E} & = & 4 \pi i \frac{\omega}{c^2} j_{e}, \end{eqnarray} where ${\bf E}$ is the perturbed electric field, ${\bf j}_e$ is the (localized) external, current source (which is responsible for generating the waves), and $\epsilon$ is the dielectric tensor. FWRD has been successfully applied to describe low-frequency waves in planetary, multi-ion magnetospheres; the results include: (i) mode-conversion at the ion-ion hybrid (IIH) resonance in Mercury [2,3]; (ii) wave coupling and mode conversion near the crossover frequency at Earth [4]; and also (iii) magnetosonic wave propagation at Earth [1].
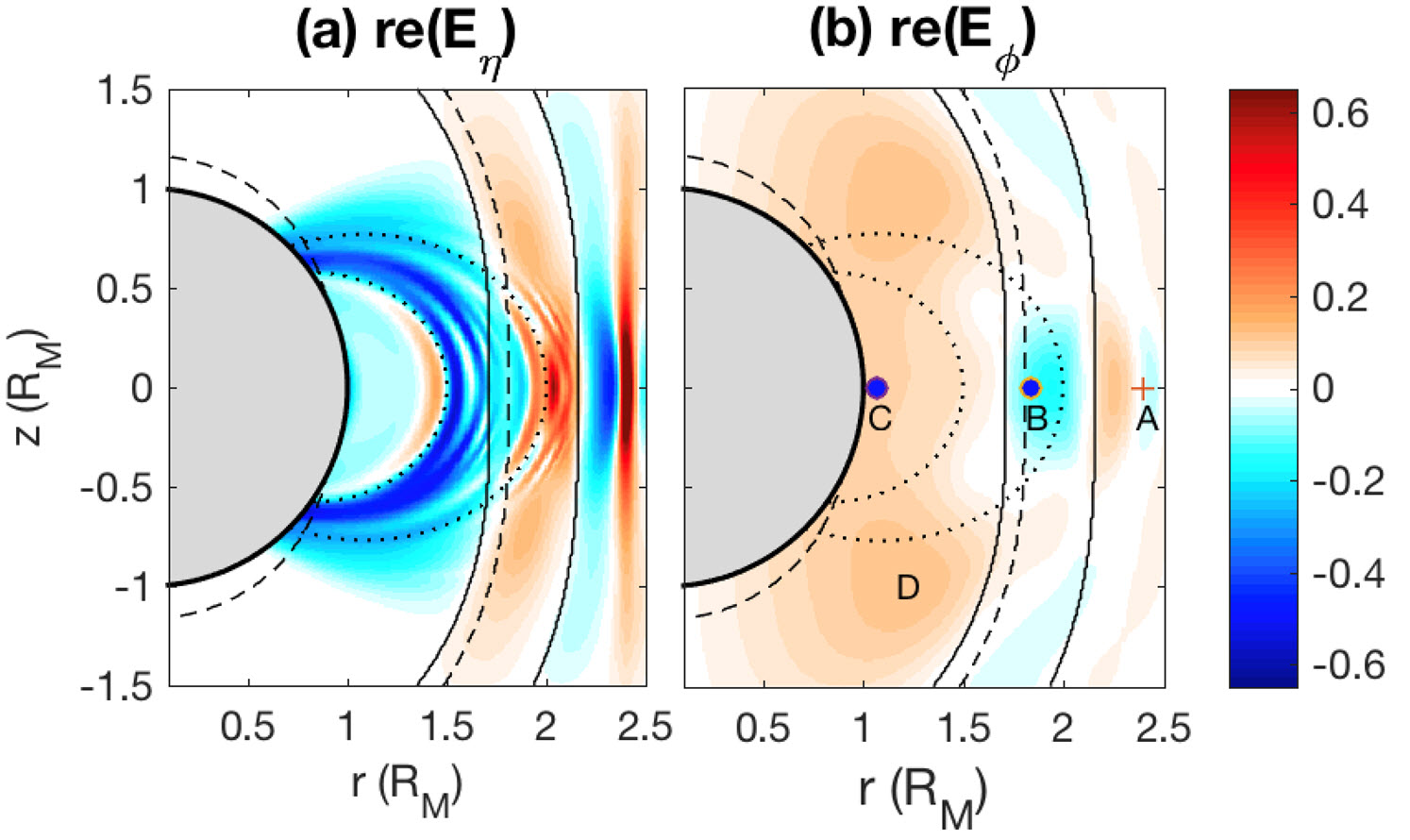
The figure (click to enlarge) shows the fluctuating electric fields in Mercury’s magnetosphere [2]; both the fast-wave and the mode-converted, IIH-resonant wave modes are shown. The fast-wave mode has a long wavelength, both across and along the magnetic fieldline, and appears in all electric and magnetic field components; the IIH-resonant waves appear only in the $E_\eta$ component, and show a long wavelength structure in the field-aligned direction and a fine structure. The waves launched at $r = 2.4 R_M$ are “pure”, fast-wave modes, and exhibit a field-aligned structure in $E_\eta$; an unmistakable evidence of mode conversion.
Some of the stongest electron precipitation and largest ionospheric ion-outflows are found in regions of intense, Alfvénic waves; thus, understanding Alfvénic aurora is crucial for our understanding of magnetosphere-ionosphere coupling and space weather. Alfvénic waves occur on a range of scales, and recent analysis [1] of auroral turbulence suggests that large-scale, global waves couple energy to small scale lengths.
We performed the first two-dimensional, self-consistent, hybrid MHD-kinetic electron simulation study of electron acceleration in a global-scale, Alfvén wave (also known as a field line resonance) for realistic plasma sheet electron temperatures in a dipolar geometry [2]; and found that mirror force effects are particularly important in the generation of the parallel electric field needed to accelerate these particles to keV energies in these global scale waves, and that this acceleration can be a major sink of wave energy, leading to significant wave damping on the order of the Alfvén period. Kinetic electron effects in-turn cause the fragmentation of the global current system into small-scale structure across the magnetic field (as shown in the figure (right panel, click to enlarge). We contrast the parallel current density in the northern hemisphere of the simulation domain for the hybrid case with kinetic electrons (right panel) and the MHD case without kinetic electrons (left panel).
Apparent in the figure is that the current layer has broadened in the hybrid case relative to the MHD. The mirror-force-induced parallel-electric-field leads to a strong cross-field Poynting flux that disperses wave energy across field lines and broadens the current profile [3]. Our model has recently been advanced to include ion Larmor radius effects (important in the equatorial region), and to study electron acceleration associated with dispersive-scale Alfvenic waves that are prevalent at the onset of substorms [4].